《2025年名校课堂九年级数学上册人教版江西专版》

1. 下列基本图形中，经过平移、旋转或轴对称变换后，不能得到左图的是(C)

答案： C

2. 观察下图，在下列四种图形变换中，该图案不包含的变换是(D)

A.旋转
B.轴对称
C.轴对称和旋转
D.平移

答案： D

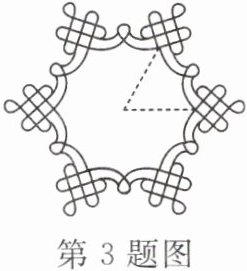
3. 第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图，这个图案绕着它的中心旋转$\alpha(0^{\circ}＜\alpha＜360^{\circ})$后能够与它本身重合，则$\alpha$可以为60(答案不唯一)$^{\circ}$.(写出一个即可)

答案： 60(答案不唯一)

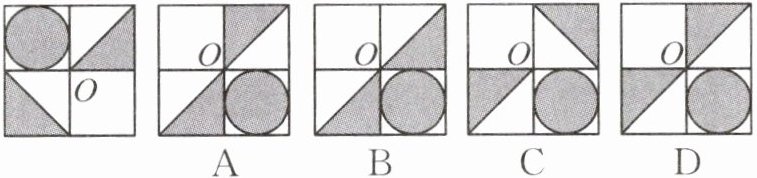
4. 如图，将正方形图案绕中心$O$逆时针旋转$180^{\circ}$后，得到的图案是(C)

答案： C

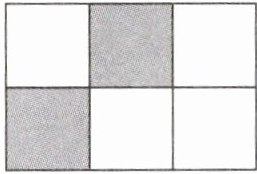
5. 如图，在$3×2$的正方形网格中，已有两个小正方形被涂黑，再将其余小正方形涂黑一个，则使整个图案构成一个轴对称图形的涂法有1种.

答案： 1

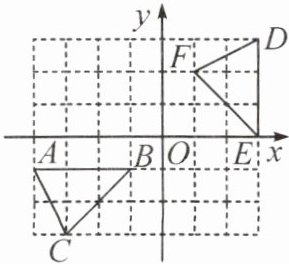
6. 如图，写出一种由$\triangle ABC$到$\triangle DEF$的变换方式：先向右平移4个单位长度,再向上平移1个单位长度,然后绕点B顺时针旋转90°.

答案： 先向右平移4个单位长度,再向上平移1个单位长度,然后绕点B顺时针旋转90°

7. 数学活动课上，张老师组织同学们设计多姿多彩的几何图形，如图都是由边长为$1$的小等边三角形构成的网格，每个网格图中有$3$个小等边三角形已涂上阴影，请同学们在余下的空白小等边三角形中选取一个涂上阴影，使得$4$个阴影小等边三角形组成一个轴对称图形或中心对称图形，请画出$4$种不同的设计图形.（规定：凡通过旋转能重合的图形视为同一种图形）

答案： 第四个三角形的位置如下（用阴影表示）：
第一个网格：与原阴影三角形关于对称轴对称（在原阴影三角形的对称位置涂上阴影）。
第二个网格：使得四个阴影三角形组成中心对称图形（在中心对称的位置涂上阴影）。
第三个网格：另一种轴对称的位置（在另一对称位置涂上阴影）。
第四个网格：再一种中心对称或轴对称的位置（根据图形对称性选择合适位置涂上阴影）。
（由于无法直接画图，以下用文字描述位置）
假设每个大三角形网格由多个小等边三角形组成，且原阴影三角形位置已知。
第一种设计：在每个大网格中，找到与原阴影三角形关于垂直中线对称的小三角形涂上阴影。
第二种设计：在每个大网格中，找到与原阴影三角形关于水平中线对称的小三角形涂上阴影（如果存在）。
第三种设计：在每个大网格中，找到与原阴影三角形关于中心点对称的小三角形涂上阴影。
第四种设计：在每个大网格中，选择一个与原阴影三角形不重复且能与其他阴影三角形组成轴对称或中心对称图形的小三角形涂上阴影（例如，关于另一条对角线对称）。
由于实际图形未给出，具体位置需根据实际图形确定，但应满足轴对称或中心对称的条件。
最终答案为四种不同的阴影设计位置（需在实际图形中标出）。

8. (1)如图$1$，在方格纸中如何通过平移或旋转这两种变换，由图形$A$得到图形$B$，再由图形$B$得到图形$C$（对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转中心、旋转方向和旋转角度）？
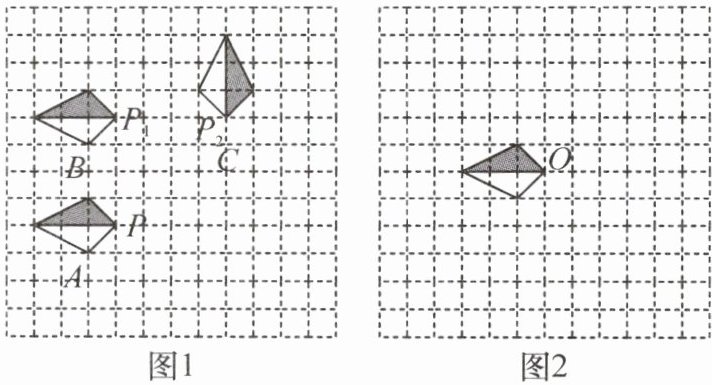
(2)图$2$是某设计师设计图案的一部分，请你运用旋转变换的方法，在方格纸中将图形绕点$O$顺时针依次旋转$90^{\circ},180^{\circ},270^{\circ}$，依次画出旋转后所得到的图形，你会得到一个美丽的图案，但涂阴影时不要涂错了位置，否则不会出现理想的效果，你来试一试吧！

答案： 解:
(1)图形A向上平移4格得到图形B;图形B以点P₁为旋转中心,顺时针旋转90°后,再向右平移4格得到图形C.
(2)图略.