第80页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. (2024·江西师大附中期中)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形,又是中心对称图形的是 (
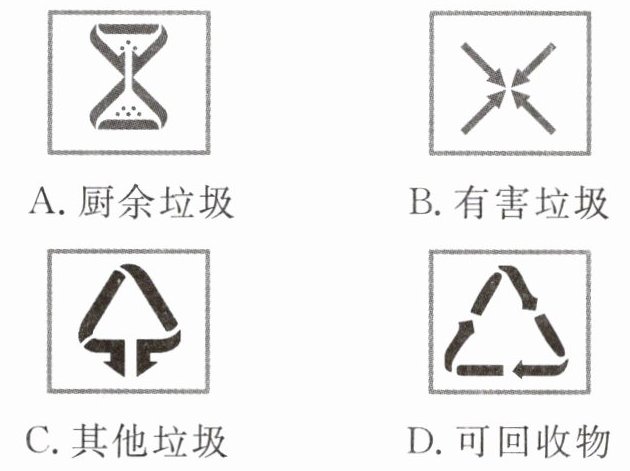
B
)
答案:
B
2. 如图,在正方形网格中,将△ABC 绕某点旋转一定的角度得到△A'B'C',则旋转中心是点 (
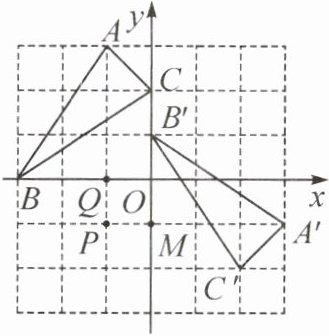
A.O
B.P
C.Q
D.M
B
)
A.O
B.P
C.Q
D.M
答案:
B
3. 在平面直角坐标系中,点 P(4,1)关于点(2,0)成中心对称的点的坐标是
(0,-1)
.
答案:
(0,-1)
4. (2023·赣州期末)若点 P(x,-3)与点 Q(4,y)关于原点对称,则 x + y =
-1
.
答案:
-1
5. (2020·江西)如图,在正方形网格中,△ABC 的顶点在格点(网格线的交点)上.请仅用无刻度直尺完成以下作图(保留作图痕迹):
(1)在图 1 中作△ABC 关于点 O 对称的△A'B'C'.
(2)在图 2 中作△ABC 绕点 A 顺时针旋转一定角度后,顶点仍在格点上的△AB'C'.
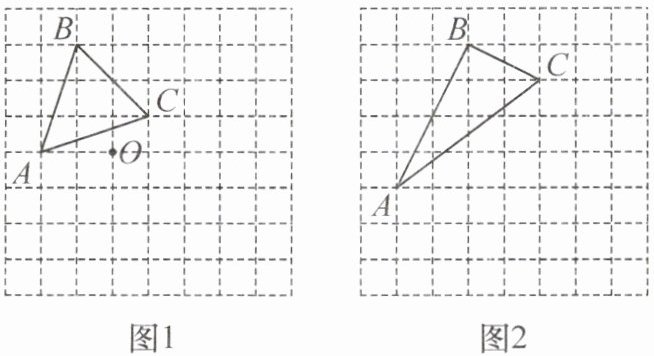
(1)在图 1 中作△ABC 关于点 O 对称的△A'B'C'.
(2)在图 2 中作△ABC 绕点 A 顺时针旋转一定角度后,顶点仍在格点上的△AB'C'.

答案:
1. (1)
步骤:
连接$AO$并延长到$A'$,使$OA' = OA$;
连接$BO$并延长到$B'$,使$OB' = OB$;
连接$CO$并延长到$C'$,使$OC' = OC$;
连接$A'B'$,$B'C'$,$C'A'$,则$\triangle A'B'C'$就是$\triangle ABC$关于点$O$对称的三角形。
2. (2)
步骤:
因为正方形网格边长相等,$AB$绕点$A$顺时针旋转$90^{\circ}$,根据网格特点找到$B$绕$A$顺时针旋转$90^{\circ}$后的格点$B'$($AB$横向占$2$格,纵向占$3$格,旋转后横向占$3$格,纵向占$2$格且方向改变);
同样的方法找到$C$绕$A$顺时针旋转$90^{\circ}$后的格点$C'$($AC$横向占$3$格,纵向占$1$格,旋转后横向占$1$格,纵向占$3$格且方向改变);
连接$AB'$,$AC'$,$B'C'$,则$\triangle AB'C'$就是$\triangle ABC$绕点$A$顺时针旋转一定角度($90^{\circ}$)后,顶点仍在格点上的三角形。
(由于是作图题,这里主要是描述作图方法,实际考试中按上述思路用直尺作图即可)
步骤:
连接$AO$并延长到$A'$,使$OA' = OA$;
连接$BO$并延长到$B'$,使$OB' = OB$;
连接$CO$并延长到$C'$,使$OC' = OC$;
连接$A'B'$,$B'C'$,$C'A'$,则$\triangle A'B'C'$就是$\triangle ABC$关于点$O$对称的三角形。
2. (2)
步骤:
因为正方形网格边长相等,$AB$绕点$A$顺时针旋转$90^{\circ}$,根据网格特点找到$B$绕$A$顺时针旋转$90^{\circ}$后的格点$B'$($AB$横向占$2$格,纵向占$3$格,旋转后横向占$3$格,纵向占$2$格且方向改变);
同样的方法找到$C$绕$A$顺时针旋转$90^{\circ}$后的格点$C'$($AC$横向占$3$格,纵向占$1$格,旋转后横向占$1$格,纵向占$3$格且方向改变);
连接$AB'$,$AC'$,$B'C'$,则$\triangle AB'C'$就是$\triangle ABC$绕点$A$顺时针旋转一定角度($90^{\circ}$)后,顶点仍在格点上的三角形。
(由于是作图题,这里主要是描述作图方法,实际考试中按上述思路用直尺作图即可)
6. (2021·江西)已知正方形 ABCD 的边长为 4 个单位长度,点 E 是 CD 的中点,请仅用无刻度直尺按下列要求作图(保留作图痕迹).
(1)在图 1 中,将直线 AC 绕着正方形 ABCD 的中心顺时针旋转 45°.
(2)在图 2 中,将直线 AC 向上平移 1 个单位长度.

(1)在图 1 中,将直线 AC 绕着正方形 ABCD 的中心顺时针旋转 45°.
(2)在图 2 中,将直线 AC 向上平移 1 个单位长度.

答案:
1. (1)
步骤:
连接$BD$,$AC$与$BD$相交于点$O$(正方形$ABCD$的中心)。
连接$AE$,$BE$。因为正方形边长为$4$,点$E$是$CD$中点,所以$DE = CE=2$,$AD = 4$,$AB = 4$。根据勾股定理$AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$,$BE=\sqrt{BC^{2}+CE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$,且$AB = 4$,$AE = BE$,$\triangle ABE$是等腰三角形。
因为$O$是$BD$中点,根据等腰三角形三线合一,$EO$平分$\angle AEB$。又因为$\angle AEB = 90^{\circ}$($\triangle ADE\cong\triangle BCE$,$\angle DAE+\angle AED = 90^{\circ}$,$\angle DAE=\angle CBE$,$\angle AED+\angle BEC = 90^{\circ}$),所以$\angle AEO = 45^{\circ}$。
作直线$EO$,直线$EO$就是将直线$AC$绕着正方形$ABCD$的中心顺时针旋转$45^{\circ}$得到的直线。
2. (2)
步骤:
取$AD$中点$F$,$BC$中点$G$(因为正方形边长为$4$,所以$AF=FD = BG=GC = 2$)。
连接$FG$,$FG$与$AC$平行(因为$AD// BC$,$AF = BG$,$FD = GC$,四边形$AFGB$和$FGCD$是平行四边形)。
过$E$作$EH// FG$交$AB$于$H$,$EH$就是将直线$AC$向上平移$1$个单位长度得到的直线(因为$E$是$CD$中点,$CD = 4$,$FG$到$EH$的距离为$1$)。
综上,(1)按上述方法作出直线$EO$;(2)按上述方法作出直线$EH$。
步骤:
连接$BD$,$AC$与$BD$相交于点$O$(正方形$ABCD$的中心)。
连接$AE$,$BE$。因为正方形边长为$4$,点$E$是$CD$中点,所以$DE = CE=2$,$AD = 4$,$AB = 4$。根据勾股定理$AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$,$BE=\sqrt{BC^{2}+CE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$,且$AB = 4$,$AE = BE$,$\triangle ABE$是等腰三角形。
因为$O$是$BD$中点,根据等腰三角形三线合一,$EO$平分$\angle AEB$。又因为$\angle AEB = 90^{\circ}$($\triangle ADE\cong\triangle BCE$,$\angle DAE+\angle AED = 90^{\circ}$,$\angle DAE=\angle CBE$,$\angle AED+\angle BEC = 90^{\circ}$),所以$\angle AEO = 45^{\circ}$。
作直线$EO$,直线$EO$就是将直线$AC$绕着正方形$ABCD$的中心顺时针旋转$45^{\circ}$得到的直线。
2. (2)
步骤:
取$AD$中点$F$,$BC$中点$G$(因为正方形边长为$4$,所以$AF=FD = BG=GC = 2$)。
连接$FG$,$FG$与$AC$平行(因为$AD// BC$,$AF = BG$,$FD = GC$,四边形$AFGB$和$FGCD$是平行四边形)。
过$E$作$EH// FG$交$AB$于$H$,$EH$就是将直线$AC$向上平移$1$个单位长度得到的直线(因为$E$是$CD$中点,$CD = 4$,$FG$到$EH$的距离为$1$)。
综上,(1)按上述方法作出直线$EO$;(2)按上述方法作出直线$EH$。
7. (2023·南昌期中)如图,将△ABC 绕点 A 顺时针旋转 120°得到△AB'C'.若点 C,B,C'共线,则∠ACB 的度数为 (
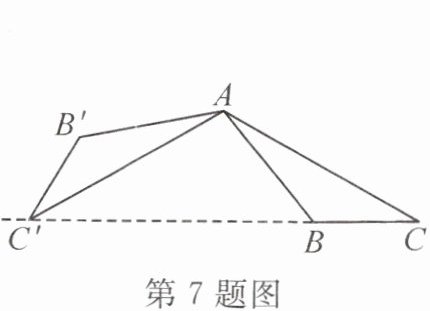
A.60°
B.45°
C.30°
D.15°
C
)
A.60°
B.45°
C.30°
D.15°
答案:
C
8. 如图,在△ABC 中,AB = AC.若 M 是边 BC 上任意一点,将△ABM 绕点 A 逆时针旋转得到△ACN,点 M 的对应点为 N,连接 MN,则下列结论一定正确的是 (

A.AB = AN
B.AB // NC
C.∠AMN = ∠ACN
D.MN ⊥ AC
C
)
A.AB = AN
B.AB // NC
C.∠AMN = ∠ACN
D.MN ⊥ AC
答案:
C
查看更多完整答案,请扫码查看


