第104页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 一个正多边形的中心角为 $30^{\circ}$,这个正多边形的边数是(
A.3
B.6
C.8
D.12
D
)A.3
B.6
C.8
D.12
答案:
D
2. 如图,正五边形 $ABCDE$ 内接于 $\odot O$,连接 $OC$,$OD$,则 $\angle COD =$(
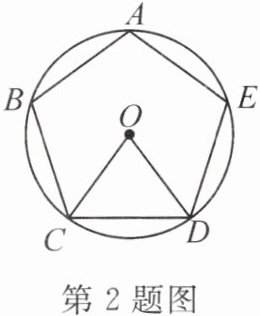
A.$72^{\circ}$
B.$60^{\circ}$
C.$54^{\circ}$
D.$48^{\circ}$
A
)
A.$72^{\circ}$
B.$60^{\circ}$
C.$54^{\circ}$
D.$48^{\circ}$
答案:
A
3. (2022·成都)如图,正六边形 $ABCDEF$ 内接于 $\odot O$。若 $\odot O$ 的周长等于 $6\pi$,则正六边形的边长为(
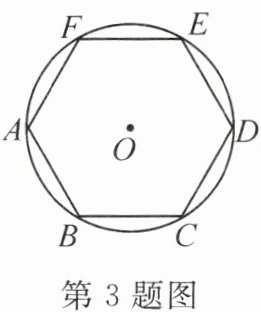
A.$\sqrt{3}$
B.$\sqrt{6}$
C.3
D.$2\sqrt{3}$
C
)
A.$\sqrt{3}$
B.$\sqrt{6}$
C.3
D.$2\sqrt{3}$
答案:
C
4. 如图,正六边形 $ABCDEF$ 内接于 $\odot O$,半径为 4,则圆心 $O$ 到 $BC$ 的距离 $OM$ 为(
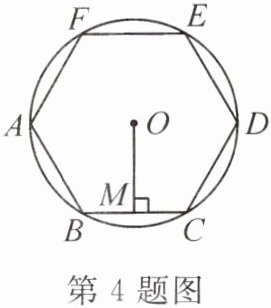
A.2
B.$2\sqrt{3}$
C.$\sqrt{3}$
D.1
B
)
A.2
B.$2\sqrt{3}$
C.$\sqrt{3}$
D.1
答案:
B
5. 在半径为 5 的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为
$5\sqrt{2}$
。
答案:
$5\sqrt{2}$
6. 如图,$B$ 是 $\odot O$ 上一点,$AC$ 为 $\odot O$ 内接正九边形的一边,则 $\angle ABC$ 的度数为
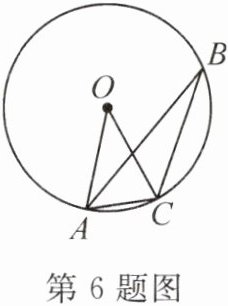
$20^{\circ }$
。
答案:
$20^{\circ }$
7. 如图,点 $O$ 是正八边形 $A_1A_2\cdots A_8$ 外接圆的圆心,连接 $A_4A_6$。若 $\odot O$ 的半径为 $4\mathrm{cm}$,则 $A_4A_6 =$
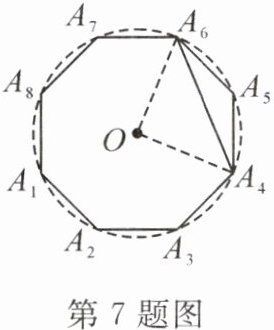
$4\sqrt{2}$
$\mathrm{cm}$。
答案:
$4\sqrt{2}$
8. (教材 P108 习题 T5 变式)如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 $b = 3\mathrm{cm}$,则螺帽边长 $a =$
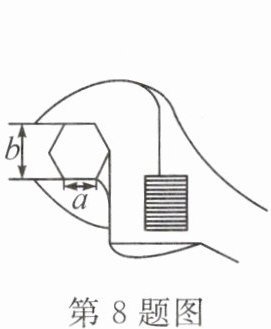
$\sqrt{3}\ cm$
。
答案:
$\sqrt{3}\ cm$
9. 如图,$\odot O$ 的半径为 $R$,六边形 $ABCDEF$ 是圆内接正六边形,四边形 $EFGH$ 是正方形。
(1)求 $\angle OGF$ 的度数。
(2)求正六边形与正方形的面积比。

(1)求 $\angle OGF$ 的度数。
(2)求正六边形与正方形的面积比。

答案:
解:
(1)$\because \angle OFE=60^{\circ },\angle EFG=90^{\circ },\therefore \angle OFG=150^{\circ }$.$\because OF=EF=FG,\therefore \angle OGF=\frac{180^{\circ }-\angle OFG}{2}=15^{\circ }$.
(2)$S_{正六边形}=6×\frac{1}{2}× R×\frac{\sqrt{3}}{2}R=\frac{3\sqrt{3}}{2}R^{2}$,$S_{正方形}=R^{2}$,$\therefore \frac{S_{正六边形}}{S_{正方形}}=\frac{\frac{3\sqrt{3}}{2}R^{2}}{R^{2}}=\frac{3\sqrt{3}}{2}$.
(1)$\because \angle OFE=60^{\circ },\angle EFG=90^{\circ },\therefore \angle OFG=150^{\circ }$.$\because OF=EF=FG,\therefore \angle OGF=\frac{180^{\circ }-\angle OFG}{2}=15^{\circ }$.
(2)$S_{正六边形}=6×\frac{1}{2}× R×\frac{\sqrt{3}}{2}R=\frac{3\sqrt{3}}{2}R^{2}$,$S_{正方形}=R^{2}$,$\therefore \frac{S_{正六边形}}{S_{正方形}}=\frac{\frac{3\sqrt{3}}{2}R^{2}}{R^{2}}=\frac{3\sqrt{3}}{2}$.
10. 图 1 是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形。
如图 2,$AE$ 是 $\odot O$ 的直径,用直尺和圆规作 $\odot O$ 内接正八边形 $ABCDEFGH$(不写作法,保留作图痕迹)。
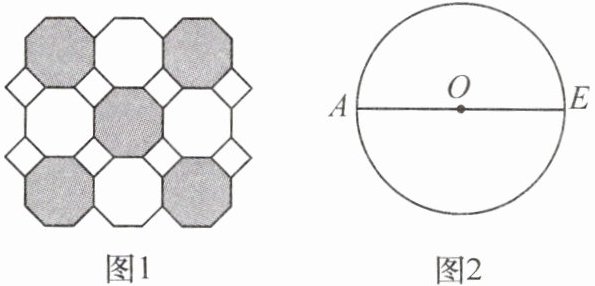
如图 2,$AE$ 是 $\odot O$ 的直径,用直尺和圆规作 $\odot O$ 内接正八边形 $ABCDEFGH$(不写作法,保留作图痕迹)。

答案:
1. 作直径AE(已知);
2. 作AE的垂直平分线,交⊙O于点C、G;
3. 分别作∠AOC、∠COE、∠EOG、∠GOA的角平分线,交⊙O于点B、D、F、H;
4. 顺次连接点A、B、C、D、E、F、G、H,得到⊙O内接正八边形ABCDEFGH。
(作图痕迹:保留作垂直平分线的弧痕、作角平分线的弧痕及各交点)
2. 作AE的垂直平分线,交⊙O于点C、G;
3. 分别作∠AOC、∠COE、∠EOG、∠GOA的角平分线,交⊙O于点B、D、F、H;
4. 顺次连接点A、B、C、D、E、F、G、H,得到⊙O内接正八边形ABCDEFGH。
(作图痕迹:保留作垂直平分线的弧痕、作角平分线的弧痕及各交点)
查看更多完整答案,请扫码查看


