第76页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
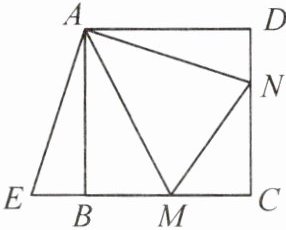
3. 如图,点$M$,$N$分别在正方形$ABCD$的边$BC$,$CD$上,且$\angle MAN = 45^{\circ}$.把$\triangle ADN$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle ABE$.
(1)求证:$\triangle AEM\cong\triangle ANM$.
(2)若$BM = 3$,$DN = 2$,求正方形$ABCD$的边长.
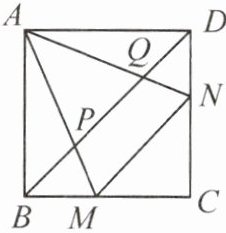
【拓展提问】在上题中,连接$BD$分别交$AM$,$AN$于点$P$,$Q$,你还能用旋转的思想说明$BP^{2}+DQ^{2}=PQ^{2}$吗?
(1)求证:$\triangle AEM\cong\triangle ANM$.
(2)若$BM = 3$,$DN = 2$,求正方形$ABCD$的边长.

【拓展提问】在上题中,连接$BD$分别交$AM$,$AN$于点$P$,$Q$,你还能用旋转的思想说明$BP^{2}+DQ^{2}=PQ^{2}$吗?

答案:
3.解:
(1)证明:由旋转的性质,得$\triangle ADN\cong \triangle ABE$,$\therefore \angle DAN=\angle BAE$,$AE=AN$,$\angle D=\angle ABE=90^{\circ}$.$\because$四边形$ABCD$是正方形,$\therefore \angle ABC=\angle BAD=90^{\circ}$.$\therefore \angle ABC+\angle ABE=180^{\circ}$.$\therefore E$,$B$,$C$三点共线.$\because \angle DAB=90^{\circ}$,$\angle MAN=45^{\circ}$,$\therefore \angle MAE=\angle BAE+\angle BAM=\angle DAN+\angle BAM=45^{\circ}$.$\therefore \angle MAE=\angle MAN$.又$\because MA=MA$,$\therefore \triangle AEM\cong \triangle ANM(SAS)$.
(2)设$CD=BC=x$,则$CM=x-3$,$CN=x-2$.$\because \triangle AEM\cong \triangle ANM$,$\therefore EM=MN$.$\because BE=DN$,$\therefore MN=BM+DN=5$.$\because \angle C=90^{\circ}$,$\therefore MN^{2}=CM^{2}+CN^{2}$.$\therefore 25=(x-3)^{2}+(x-2)^{2}$,解得$x=6$或$x=-1$(舍去).$\therefore$正方形$ABCD$的边长为$6$.
【拓展提问】解:$\because$四边形$ABCD$为正方形,$\therefore \angle ABD=\angle ADB=45^{\circ}$.将$\triangle ADQ$绕点$A$按顺时针方向旋转$90^{\circ}$,则$AD$与$AB$重合,得到$\triangle ABK$,连接$KP$.则$\angle ABK=\angle ADQ=45^{\circ}$,$BK=DQ$,$AK=AQ$.同理可证$\triangle APQ\cong \triangle APK$,得到$PQ=PK$.$\because \angle PBK=\angle PBA+\angle KBA=45^{\circ}+45^{\circ}=90^{\circ}$,$\therefore \triangle BPK$为直角三角形.$\therefore BP^{2}+BK^{2}=PK^{2}$.$\therefore BP^{2}+DQ^{2}=PQ^{2}$.
(1)证明:由旋转的性质,得$\triangle ADN\cong \triangle ABE$,$\therefore \angle DAN=\angle BAE$,$AE=AN$,$\angle D=\angle ABE=90^{\circ}$.$\because$四边形$ABCD$是正方形,$\therefore \angle ABC=\angle BAD=90^{\circ}$.$\therefore \angle ABC+\angle ABE=180^{\circ}$.$\therefore E$,$B$,$C$三点共线.$\because \angle DAB=90^{\circ}$,$\angle MAN=45^{\circ}$,$\therefore \angle MAE=\angle BAE+\angle BAM=\angle DAN+\angle BAM=45^{\circ}$.$\therefore \angle MAE=\angle MAN$.又$\because MA=MA$,$\therefore \triangle AEM\cong \triangle ANM(SAS)$.
(2)设$CD=BC=x$,则$CM=x-3$,$CN=x-2$.$\because \triangle AEM\cong \triangle ANM$,$\therefore EM=MN$.$\because BE=DN$,$\therefore MN=BM+DN=5$.$\because \angle C=90^{\circ}$,$\therefore MN^{2}=CM^{2}+CN^{2}$.$\therefore 25=(x-3)^{2}+(x-2)^{2}$,解得$x=6$或$x=-1$(舍去).$\therefore$正方形$ABCD$的边长为$6$.
【拓展提问】解:$\because$四边形$ABCD$为正方形,$\therefore \angle ABD=\angle ADB=45^{\circ}$.将$\triangle ADQ$绕点$A$按顺时针方向旋转$90^{\circ}$,则$AD$与$AB$重合,得到$\triangle ABK$,连接$KP$.则$\angle ABK=\angle ADQ=45^{\circ}$,$BK=DQ$,$AK=AQ$.同理可证$\triangle APQ\cong \triangle APK$,得到$PQ=PK$.$\because \angle PBK=\angle PBA+\angle KBA=45^{\circ}+45^{\circ}=90^{\circ}$,$\therefore \triangle BPK$为直角三角形.$\therefore BP^{2}+BK^{2}=PK^{2}$.$\therefore BP^{2}+DQ^{2}=PQ^{2}$.
4. 如图,在四边形$ABCD$中,$AB = AD$,$\angle B = \angle D = 90^{\circ}$,$\angle BAD = 120^{\circ}$,以$A$为顶点的$\angle EAF = 60^{\circ}$,$AE$,$AF$与$BC$,$CD$边分别交于$E$,$F$两点.试判断$EF$,$BE$和$DF$之间的数量关系,并说明理由.


答案:
4.解:$EF=DF+BE$.理由:将$\triangle ADF$绕点$A$顺时针旋转$120^{\circ}$得到$\triangle ABM$,$\therefore \triangle ABM\cong \triangle ADF$,$\therefore \angle ABM=\angle D=90^{\circ}$,$\angle MAB=\angle FAD$,$AM=AF$,$MB=DF$.$\therefore \angle ABM+\angle ABE=180^{\circ}$.$\therefore M$,$B$,$E$三点共线.$\because \angle MAE=\angle MAB+\angle BAE=\angle FAD+\angle BAE=\angle BAD-\angle EAF=60^{\circ}$,$\therefore \angle MAE=\angle FAE$.又$\because AE=AE$,$AM=AF$,$\therefore \triangle MAE\cong \triangle FAE(SAS)$.$\therefore ME=EF$.$\therefore EF=ME=MB+BE=DF+BE$.
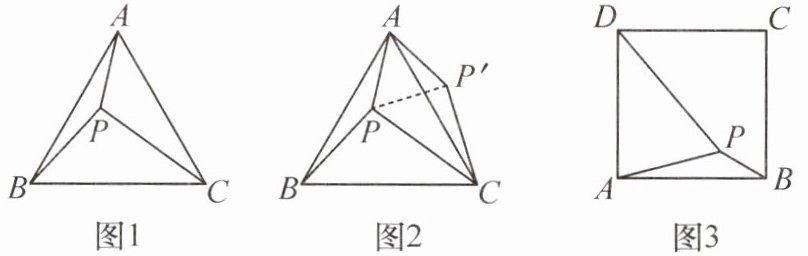
5. 小伟遇到这样一个问题:如图 1,在等边三角形$ABC$内有一点$P$,且$PA = 3$,$PB = 4$,$PC = 5$,求$\angle APB$的度数.
小伟是这样思考的:如图 2,利用旋转和全等的知识构造$\triangle AP'C$,连接$PP'$,得到两个特殊的三角形,从而将问题解决.
参考小伟同学的方法,解决下列问题.
(1)图 1 中$\angle APB$的度数为
(2)如图 3,在正方形$ABCD$内有一点$P$,且$PA = 2\sqrt{2}$,$PB = 1$,$PD = \sqrt{17}$,求$\angle APB$的度数以及正方形$ABCD$的边长.
小伟是这样思考的:如图 2,利用旋转和全等的知识构造$\triangle AP'C$,连接$PP'$,得到两个特殊的三角形,从而将问题解决.
参考小伟同学的方法,解决下列问题.
(1)图 1 中$\angle APB$的度数为
150°
.(2)如图 3,在正方形$ABCD$内有一点$P$,且$PA = 2\sqrt{2}$,$PB = 1$,$PD = \sqrt{17}$,求$\angle APB$的度数以及正方形$ABCD$的边长.

答案:
5.解:
(1)$150^{\circ}$
(2)把$\triangle APB$绕点$A$逆时针旋转$90^{\circ}$得到$\triangle ADP'$,连接$PP'$.由旋转的性质,得$P'A=PA=2\sqrt{2}$,$P'D=PB=1$,$\angle PAP'=90^{\circ}$,$\angle AP'D=\angle APB$,$\therefore \triangle APP'$是等腰直角三角形.$\therefore PP'=\sqrt{2}PA=4$,$\angle AP'P=45^{\circ}$.$\because PP'^{2}+P'D^{2}=4^{2}+1^{2}=17$,$PD^{2}=(\sqrt{17})^{2}=17$,$\therefore PP'^{2}+P'D^{2}=PD^{2}$.$\therefore \angle PP'D=90^{\circ}$.$\therefore \angle AP'D=\angle AP'P+\angle PP'D=45^{\circ}+90^{\circ}=135^{\circ}$.$\therefore \angle APB=\angle AP'D=135^{\circ}$.$\therefore \angle APP'+\angle APB=180^{\circ}$,即$P'$,$P$,$B$三点共线.过点$A$作$AE\perp PP'$,则$AE=EP=2$,$BE=1+2=3$.在$Rt\triangle AEB$中,$AB=\sqrt{AE^{2}+EB^{2}}=\sqrt{13}$.$\therefore$正方形$ABCD$的边长为$\sqrt{13}$.
(1)$150^{\circ}$
(2)把$\triangle APB$绕点$A$逆时针旋转$90^{\circ}$得到$\triangle ADP'$,连接$PP'$.由旋转的性质,得$P'A=PA=2\sqrt{2}$,$P'D=PB=1$,$\angle PAP'=90^{\circ}$,$\angle AP'D=\angle APB$,$\therefore \triangle APP'$是等腰直角三角形.$\therefore PP'=\sqrt{2}PA=4$,$\angle AP'P=45^{\circ}$.$\because PP'^{2}+P'D^{2}=4^{2}+1^{2}=17$,$PD^{2}=(\sqrt{17})^{2}=17$,$\therefore PP'^{2}+P'D^{2}=PD^{2}$.$\therefore \angle PP'D=90^{\circ}$.$\therefore \angle AP'D=\angle AP'P+\angle PP'D=45^{\circ}+90^{\circ}=135^{\circ}$.$\therefore \angle APB=\angle AP'D=135^{\circ}$.$\therefore \angle APP'+\angle APB=180^{\circ}$,即$P'$,$P$,$B$三点共线.过点$A$作$AE\perp PP'$,则$AE=EP=2$,$BE=1+2=3$.在$Rt\triangle AEB$中,$AB=\sqrt{AE^{2}+EB^{2}}=\sqrt{13}$.$\therefore$正方形$ABCD$的边长为$\sqrt{13}$.
查看更多完整答案,请扫码查看


