第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
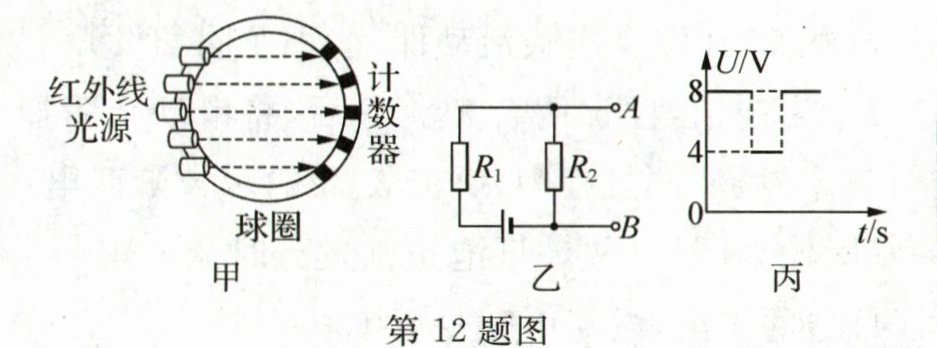
12. (2025·福建厦门期中)抛绣球是壮族人民喜爱的民俗活动之一.小天设计了一个自动记录绣球过圈数量的计数器(如图甲),其简化电路如图乙.其中$R_{1}$是光敏电阻,当绣球挡住了射向$R_{1}$的红外线时,$R_{1}$的阻值会变小为10Ω,A、B间电压变大,这时自动计数器计数一次.已知$R_{2}$是定值电阻,电源电压恒为12V,当绣球穿过球圈时,A、B间的电压随时间变化的图像如图乙,则$R_{2}$的阻值为______Ω;当没有绣球通过球圈,红外线正常照射$R_{1}$时,$R_{1}$的阻值为______Ω.

答案:
20 40 解析:由图乙可知,$R_{1}$、$R_{2}$串联,当绣球挡住了射向$R_{1}$的红外线时,$R_{1}$的阻值会变小,A、B 间电压变大,由丙图可知,$R_{1}$变小后,A、B 间输出的电压为8V,即$R_{2}$两端的电压$U_{2}=8V$,由串联电路的电压规律可得,$R_{1}$两端的电压$U_{1}=U-U_{2}=12V-8V=4V$,由串联分压可得$\frac {R_{1}}{R_{2}}=\frac {U_{1}}{U_{2}}$,即$\frac {10Ω}{R_{2}}=\frac {4V}{8V}$,解得$R_{2}=20Ω$;红外线正常照射$R_{1}$时,由图丙可知,A、B 间输出的电压为4V,即$R_{2}$两端的电压$U_{2}'=4V$,则$R_{1}$两端的电压$U_{1}'=U-U_{2}'=12V-4V=8V$,由串联分压可得$\frac {R_{1}'}{R_{2}'}=\frac {U_{1}'}{U_{2}'}$,即$\frac {R_{1}'}{20Ω}=\frac {8V}{4V}$,解得$R_{1}'=40Ω.$
13. (6分)(2025·江苏盐城期中)《天工开物》是我国古代的科学著作,书中记载着大量的古代农业机械.其中这样写道:"凡河滨有制筒车者,堰陂障流绕于车下,激轮使转,挽水入筒,一一倾于枧内,流入亩中,昼夜不息,百亩无忧."该段文字描述了筒车这种以水流作动力,用来取水的机械,如图甲.如图乙,接水槽离取水处高4m,水轮上有12个取水筒,一个取水筒每次可取水4kg,筒车旋转一周所用时间为60s.若水流冲击筒车的功率为40W(接水槽离倒水处的高度忽略不计,g取10N/kg)
(1)求该筒车旋转一周,水流冲击筒车所做的总功.
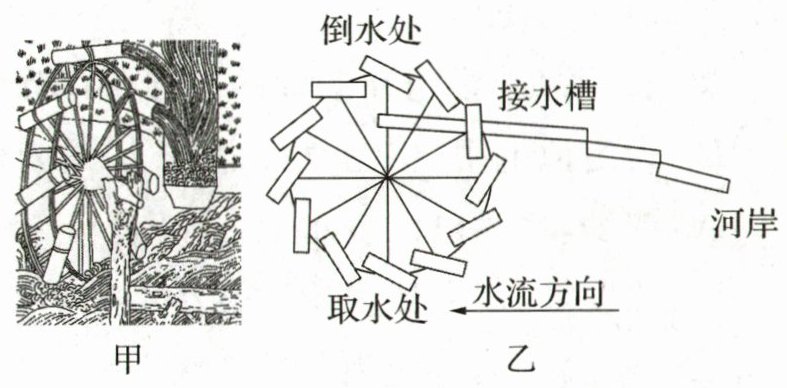
(2)求筒车旋转一周取水的机械效率.
(3)若采用效率为30%的柴油发动机代替水车旋转一小时抽相同质量的水,需要燃烧柴油的质量是多少克?(柴油的热值约为$4×10^{7}J/kg$)
(1)求该筒车旋转一周,水流冲击筒车所做的总功.

(2)求筒车旋转一周取水的机械效率.
(3)若采用效率为30%的柴油发动机代替水车旋转一小时抽相同质量的水,需要燃烧柴油的质量是多少克?(柴油的热值约为$4×10^{7}J/kg$)
答案:
(1)2400J
(2)80%
(3)9.6g 解析:
(1)水流冲击筒车所做的总功$W_{总}=Pt=40W×60s=2400J$.
(2)筒车旋转一周所做的有用功$W_{有用}=Gh=mgh=12×4kg×10N/kg×4m=1920J$,筒车旋转一周取水的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1920J}{2400J}×100\% =80\% $.
(3)用柴油发动机代替水车旋转一小时抽取相同质量的水,所做的有用功$W_{有用1}=\frac {3600s}{60s}×W_{有用}=60×1920J=1.152×10^{5}J$,燃烧柴油放出的热量$Q_{放}=\frac {W_{有用1}}{η_{1}}=\frac {1.152×10^{5}J}{30\% }=3.84×10^{5}J$,需要燃烧柴油的质量$m_{柴油}=\frac {Q_{放}}{q}=\frac {3.84×10^{5}J}{4×10^{7}J/kg}=0.0096kg=9.6g.$
(1)2400J
(2)80%
(3)9.6g 解析:
(1)水流冲击筒车所做的总功$W_{总}=Pt=40W×60s=2400J$.
(2)筒车旋转一周所做的有用功$W_{有用}=Gh=mgh=12×4kg×10N/kg×4m=1920J$,筒车旋转一周取水的机械效率$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1920J}{2400J}×100\% =80\% $.
(3)用柴油发动机代替水车旋转一小时抽取相同质量的水,所做的有用功$W_{有用1}=\frac {3600s}{60s}×W_{有用}=60×1920J=1.152×10^{5}J$,燃烧柴油放出的热量$Q_{放}=\frac {W_{有用1}}{η_{1}}=\frac {1.152×10^{5}J}{30\% }=3.84×10^{5}J$,需要燃烧柴油的质量$m_{柴油}=\frac {Q_{放}}{q}=\frac {3.84×10^{5}J}{4×10^{7}J/kg}=0.0096kg=9.6g.$
14. (6分)北京时间2024年10月30日20时59分,神舟十九号载人飞船发射.飞船发射前,通常要检验舱体的气密性,某科技小组设计的检测电路如图甲所示,电源电压恒定不变,定值电阻$R_{0}= 50Ω$,气压传感器R的阻值随环境气压的变化规律如图乙所示.进行气密性监测时,将气压传感器R置于舱体内,舱体置于真空室中,舱体不漏气时,舱体内气压为$1.0×10^{5}Pa$,此时电压表示数为10V.求:

(1)舱体不漏气时通过$R_{0}$的电流.
(2)电源电压.
(3)电压表示数为7.5V时舱体内的气压.

(1)舱体不漏气时通过$R_{0}$的电流.
(2)电源电压.
(3)电压表示数为7.5V时舱体内的气压.
答案:
(1)0.2A
(2)12V
(3)$4×10^{4}Pa$ 解析:
(1)由图甲可知,定值电阻$R_{0}$与气压传感器 R 串联接入电路,电压表测量$R_{0}$两端的电压.舱体不漏气时,电压表示数为10V,即$R_{0}$两端的电压$U_{0}=10V$,由欧姆定律可得,通过$R_{0}$的电流$I=\frac {U_{0}}{R_{0}}=\frac {10V}{50Ω}=0.2A$.
(2)由图乙可知,当舱体内气压为$1.0×10^{5}Pa$时,气压传感器阻值$R=10Ω$,此时电路的总电阻$R_{总}=R+R_{0}=10Ω+50Ω=60Ω$,由欧姆定律可得,电源电压$U=IR_{总}=0.2A×60Ω=12V$.
(3)电压表示数为7.5V时,电路中的电流$I'=\frac {U_{0}'}{R_{0}}=\frac {7.5V}{50Ω}=0.15A$,R 两端的电压$U_{R}=U-U_{0}'=12V-7.5V=4.5V$,此时气压传感器的阻值$R'=\frac {U_{R}}{I'}=\frac {4.5V}{0.15A}=30Ω$,由图乙可知,此时舱体内的气压为$0.4×10^{5}Pa=4×10^{4}Pa.$
(1)0.2A
(2)12V
(3)$4×10^{4}Pa$ 解析:
(1)由图甲可知,定值电阻$R_{0}$与气压传感器 R 串联接入电路,电压表测量$R_{0}$两端的电压.舱体不漏气时,电压表示数为10V,即$R_{0}$两端的电压$U_{0}=10V$,由欧姆定律可得,通过$R_{0}$的电流$I=\frac {U_{0}}{R_{0}}=\frac {10V}{50Ω}=0.2A$.
(2)由图乙可知,当舱体内气压为$1.0×10^{5}Pa$时,气压传感器阻值$R=10Ω$,此时电路的总电阻$R_{总}=R+R_{0}=10Ω+50Ω=60Ω$,由欧姆定律可得,电源电压$U=IR_{总}=0.2A×60Ω=12V$.
(3)电压表示数为7.5V时,电路中的电流$I'=\frac {U_{0}'}{R_{0}}=\frac {7.5V}{50Ω}=0.15A$,R 两端的电压$U_{R}=U-U_{0}'=12V-7.5V=4.5V$,此时气压传感器的阻值$R'=\frac {U_{R}}{I'}=\frac {4.5V}{0.15A}=30Ω$,由图乙可知,此时舱体内的气压为$0.4×10^{5}Pa=4×10^{4}Pa.$
查看更多完整答案,请扫码查看


