《2025年亮点给力大试卷九年级物理上册苏科版》

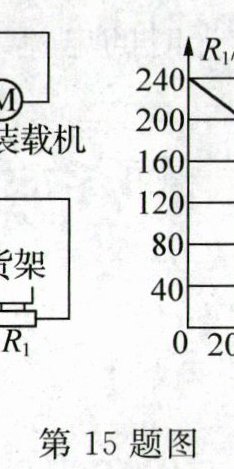
15. (5 分)图甲是跨学科实践小组用力敏电阻$ R_1$设计的一种“自动限重器”,力敏电阻$ R_1$的阻值随压力 F 变化的关系如图乙.当货架承受的压力达到限定值时,电磁继电器会自动控制货物装载机停止向货架上摆放物品.已知控制电路的电源电压 U= 6V,定值电阻$ R_2= 60Ω($货架自重和线圈电阻都忽略不计).
(1) 当货架上不放物品时$,R_1= ______Ω,$此时线圈中的电流为______A.
(2) 当线圈中的电流达到 30mA 时衔铁被吸下,则货架能承受的最大压力为______N.为了调节货架能承受的最大压力,可调整控制电路的电源电压,若需要控制货架能承受的最大压力为 800 N,则替换的电源电压为______V;若不更换电源,可将$ R_2$换成最大阻值至少为______Ω的滑动变阻器.

答案： （1）240 0.02 （2）500 4.2 120 解析:由图甲可知，力敏电阻 R₁、定值电阻 R₂和线圈串联。
(1)货架自重忽略不计，当货架上不放物品时，R₁承受的压力为 0，由图乙可知，此时 R₁ = 240 Ω，线圈电阻不计，电路的总电阻 R = R₁ + R₂ = 240 Ω + 60 Ω = 300 Ω，则此时线圈中的电流 I = $\frac{U}{R}$ = $\frac{6\ V}{300\ \Omega}$ = 0.02 A。
(2)由图乙可知，R₁的阻值与压力 F 成一次函数，设关系式为 R₁ = aF + b，则 240 Ω = a×0 + b；200 Ω = a×200 N + b，所以 a = -0.2，b = 240 Ω，则 R₁ = -0.2F + 240 Ω。当电磁继电器线圈中的电流为 Iₘₐₓ = 30 mA = 0.03 A 时衔铁被吸下，由欧姆定律可得，此时电路的最小总电阻 R' = $\frac{U}{I_{max}}$ = $\frac{6\ V}{0.03\ A}$ = 200 Ω，则此时力敏电阻的最小阻值 R₁' = R' - R₂ = 200 Ω - 60 Ω = 140 Ω。由 R₁ = -0.2F + 240 Ω 可得，140 Ω = -0.2Fₘₐₓ + 240 Ω，则此时货架能承受的最大压力 Fₘₐₓ = 500 N。若需要控制货架能承受的最大压力为 800 N，由图乙知力敏电阻对应的阻值 R₁ₘᵢₙ = 80 Ω，线圈中的电流为 30 mA 不变，此时替换的电源电压 U' = I(R₁ₘᵢₙ + R₂) = 0.03 A×(80 Ω + 60 Ω) = 4.2 V；若不更换电源，滑动变阻器 R₂的最大阻值至少为 Rₐₗₜ = R' - R₁ₘᵢₙ = 200 Ω - 80 Ω = 120 Ω。

16. (6 分)按照题目要求作图.
(1) 如图甲,在杠杆中画出其受到的阻力$ F_2$及能使其保持平衡的最小动力$ F_1$的示意图.
(2) 如图乙,用笔画线代替导线将电灯、开关和插座分别接入电路.
(3) 如图丙,标出通电螺线管周围的磁感线方向及电源的正极.

答案：
（1）如图所示
　　　　　　　
（2）如图所示
　　　　　　
（3）如图所示
　　　　　　　　

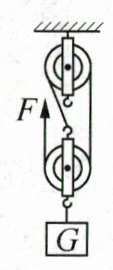
17. (6 分)如图所示的滑轮组下挂一重为 45 N 的物体,现用 20 N 的拉力 F 在 4 s 内将物体匀速提升 2 m.求:
(1) 此过程中所做的有用功.
(2) 滑轮组的机械效率.
(3) 当克服摩擦和绳重所做的功为总功的 5%时,动滑轮的重力.

答案： （1）90 J （2）75% （3）12 N 解析:
(1)此过程中所做的有用功 Wₒᵤₜ = Gh = 45 N×2 m = 90 J。
(2)由图可知，动滑轮上的绳子段数 n = 3，拉力端绳子移动的距离 s = nh = 3×2 m = 6 m，拉力做的总功 Wᵢₙ = Fs = 20 N×6 m = 120 J，则滑轮组的机械效率 η = $\frac{W_{有用}}{W_{总}}$×100% = $\frac{90\ J}{120\ J}$×100% = 75%。
(3)由题意可得，克服摩擦和绳重所做的额外功 Wₑₓₜᵣₐ₁ = 5%Wᵢₙ = 5%×120 J = 6 J，则克服动滑轮重做的额外功 Wₑₓₜᵣₐ₂ = Wᵢₙ - Wₒᵤₜ - Wₑₓₜᵣₐ₁ = 120 J - 90 J - 6 J = 24 J。由 W = Gh 可得，动滑轮的重力 Gₘ = $\frac{W_{额外2}}{h}$ = $\frac{24\ J}{2\ m}$ = 12 N。