第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
5. (2024·日照)物理学习小组研究电路的特点,一组同学按照甲电路图连接好电路后,闭合开关,电路正常工作,学生电压表 $V_{1}$ 和 $V_{2}$ 的指针偏转均如图乙所示;二组同学按照丙电路图连接电路.已知 $R_{1}= 4Ω$,两小组所用的电源和定值电阻均相同,下列判断正确的是 (
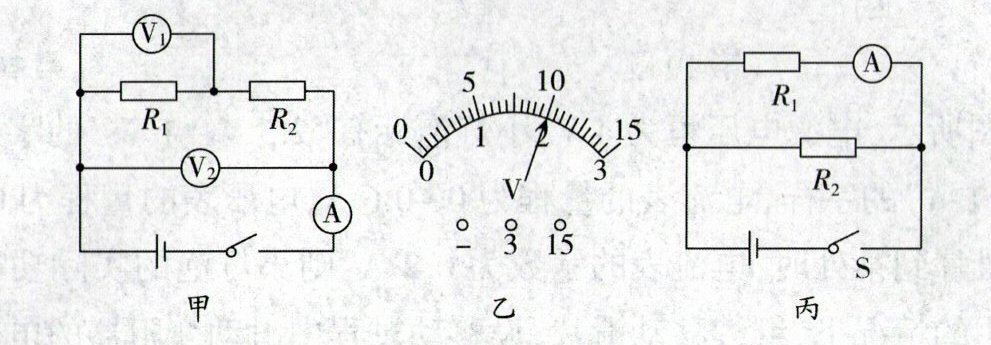
A.甲图中电流表示数为 0.6 A
B.$R_{2}$ 的阻值为 20 Ω
C.丙图中,$R_{2}$ 的电流为 0.5 A
D.丙图中,$R_{1}$ 的功率为 25 W
D
)
A.甲图中电流表示数为 0.6 A
B.$R_{2}$ 的阻值为 20 Ω
C.丙图中,$R_{2}$ 的电流为 0.5 A
D.丙图中,$R_{1}$ 的功率为 25 W
答案:
解:甲图中,$R_1$与$R_2$串联,$V_1$测$R_1$电压,$V_2$测总电压。
乙图电压表指针偏转相同,$V_2$量程为0-15V,读数10V;$V_1$量程为0-3V,读数2V。
$U=10V$,$U_1=2V$,$U_2=U-U_1=8V$。
$I=\frac{U_1}{R_1}=\frac{2V}{4\Omega}=0.5A$,$R_2=\frac{U_2}{I}=\frac{8V}{0.5A}=16\Omega$。
丙图中,$R_1$与$R_2$并联,电源电压$U=10V$。
$I_{R2}=\frac{U}{R_2}=\frac{10V}{16\Omega}=0.625A$,$P_{R1}=\frac{U^2}{R_1}=\frac{(10V)^2}{4\Omega}=25W$。
A.电流表示数0.5A,A错误;B.$R_2=16\Omega$,B错误;C.$R_2$电流0.625A,C错误;D.$R_1$功率25W,D正确。
答案:D
乙图电压表指针偏转相同,$V_2$量程为0-15V,读数10V;$V_1$量程为0-3V,读数2V。
$U=10V$,$U_1=2V$,$U_2=U-U_1=8V$。
$I=\frac{U_1}{R_1}=\frac{2V}{4\Omega}=0.5A$,$R_2=\frac{U_2}{I}=\frac{8V}{0.5A}=16\Omega$。
丙图中,$R_1$与$R_2$并联,电源电压$U=10V$。
$I_{R2}=\frac{U}{R_2}=\frac{10V}{16\Omega}=0.625A$,$P_{R1}=\frac{U^2}{R_1}=\frac{(10V)^2}{4\Omega}=25W$。
A.电流表示数0.5A,A错误;B.$R_2=16\Omega$,B错误;C.$R_2$电流0.625A,C错误;D.$R_1$功率25W,D正确。
答案:D
6. (2024·济宁)如图是一个灯泡 L 和一个定值电阻 R 的 I-U 图像.下列分析正确的是 (
A.甲为灯泡 L 的图线
B.当电压为 0 时,L 与 R 的阻值均为 0
C.将 L 和 R 并联在 6 V 的电源两端,电路总电阻为 36 Ω
D.将 L 和 R 串联在 6 V 的电源两端,L 的功率为 0.24 W
D
)A.甲为灯泡 L 的图线
B.当电压为 0 时,L 与 R 的阻值均为 0
C.将 L 和 R 并联在 6 V 的电源两端,电路总电阻为 36 Ω
D.将 L 和 R 串联在 6 V 的电源两端,L 的功率为 0.24 W
答案:
【解析】:
A选项:通过定值电阻的电流与两端电压成正比,其$U-I$图像为过原点的直线,而灯丝的电阻会随温度的变化而改变,故乙为定值电阻,甲为灯泡,故A错误。
B选项:电阻是导体本身的性质,与导体的材料、长度、横截面积以及温度有关,与电压和电流无关,当电压为0时,$L$与$R$的阻值不为0,故B错误。
C选项:并联电路中各个支路两端的电压均等于电源电压,总电流等于各支路电流之和,由图可知,当电压为6V时,$I_R$为0.5A,$I_L$为0.25A,总电流$I=I_R+I_L=0.5A+0.25A=0.75A$,总电阻$R_总=\frac{U}{I}=\frac{6V}{0.75A}=8\Omega$,故C错误。
D选项:串联电路中总电压等于各分电压之和,各处电流相等,由图可知,当电流为0.2A时,定值电阻两端的电压为4V,灯泡两端的电压为2V,满足总电压为6V,所以灯泡的功率$P_L=U_LI=2V× 0.2A=0.24W$,故D正确。
【答案】:D。
A选项:通过定值电阻的电流与两端电压成正比,其$U-I$图像为过原点的直线,而灯丝的电阻会随温度的变化而改变,故乙为定值电阻,甲为灯泡,故A错误。
B选项:电阻是导体本身的性质,与导体的材料、长度、横截面积以及温度有关,与电压和电流无关,当电压为0时,$L$与$R$的阻值不为0,故B错误。
C选项:并联电路中各个支路两端的电压均等于电源电压,总电流等于各支路电流之和,由图可知,当电压为6V时,$I_R$为0.5A,$I_L$为0.25A,总电流$I=I_R+I_L=0.5A+0.25A=0.75A$,总电阻$R_总=\frac{U}{I}=\frac{6V}{0.75A}=8\Omega$,故C错误。
D选项:串联电路中总电压等于各分电压之和,各处电流相等,由图可知,当电流为0.2A时,定值电阻两端的电压为4V,灯泡两端的电压为2V,满足总电压为6V,所以灯泡的功率$P_L=U_LI=2V× 0.2A=0.24W$,故D正确。
【答案】:D。
7. 人类进人电气化时代的重要标志是大规模使用电能.电能无法从自然界直接获取,它通常通过发电机由其他形式的能转化而来,最终通过各种用电器转化为其他形式的能.电能的生产、输送和利用,极大地促进了社会经济发展和人类文明的进步.如图为远距离输电示意图,I 为输电电流,r为输电线总电阻,U 为用户端的电压,则因输电线发热而损耗的电能为(t 为通电时间) (
A.$I^{2}rt$
B.$\frac{U^{2}t}{r}$
C.UIt
D.$UIt + I^{2}rt$
A
)A.$I^{2}rt$
B.$\frac{U^{2}t}{r}$
C.UIt
D.$UIt + I^{2}rt$
答案:
【解析】:
本题主要考查电能的损耗计算,需要理解电能损耗的原因以及掌握相关的电学公式。
首先,分析题目中给出的远距离输电示意图。电能从发电厂通过输电线输送到用户端,由于输电线存在一定的电阻$r$,因此会有部分电能转化为热能而损耗。
接下来,根据焦耳定律来计算因输电线发热而损耗的电能。焦耳定律的公式为$Q = I^{2}Rt$,其中$Q$表示热量,$I$表示电流,$R$表示电阻,$t$表示时间。在本题中,输电线总电阻为$r$,输电电流为$I$,通电时间为$t$,因此因输电线发热而损耗的电能为$I^{2}rt$。
然后,逐一分析选项:
A选项:$I^{2}rt$,符合焦耳定律的计算公式,是正确的。
B选项:$\frac{U^{2}t}{r}$,这个公式通常用于计算纯电阻电路中的电能,但本题中的输电线并非纯电阻电路,且用户端的电压$U$并不等于输电线两端的电压,因此这个公式不适用。
C选项:$UIt$,这个公式表示的是电能的总输送量,而不是损耗的电能。
D选项:$UIt + I^{2}rt$,这个公式没有实际意义,因为$UIt$表示的是总输送量,而$I^{2}rt$表示的是损耗量,两者相加没有物理意义。
【答案】:A
本题主要考查电能的损耗计算,需要理解电能损耗的原因以及掌握相关的电学公式。
首先,分析题目中给出的远距离输电示意图。电能从发电厂通过输电线输送到用户端,由于输电线存在一定的电阻$r$,因此会有部分电能转化为热能而损耗。
接下来,根据焦耳定律来计算因输电线发热而损耗的电能。焦耳定律的公式为$Q = I^{2}Rt$,其中$Q$表示热量,$I$表示电流,$R$表示电阻,$t$表示时间。在本题中,输电线总电阻为$r$,输电电流为$I$,通电时间为$t$,因此因输电线发热而损耗的电能为$I^{2}rt$。
然后,逐一分析选项:
A选项:$I^{2}rt$,符合焦耳定律的计算公式,是正确的。
B选项:$\frac{U^{2}t}{r}$,这个公式通常用于计算纯电阻电路中的电能,但本题中的输电线并非纯电阻电路,且用户端的电压$U$并不等于输电线两端的电压,因此这个公式不适用。
C选项:$UIt$,这个公式表示的是电能的总输送量,而不是损耗的电能。
D选项:$UIt + I^{2}rt$,这个公式没有实际意义,因为$UIt$表示的是总输送量,而$I^{2}rt$表示的是损耗量,两者相加没有物理意义。
【答案】:A
8. 如图所示的家庭照明电路,闭合开关 $S_{1}$、$S_{2}$ 后,灯泡 $L_{1}$ 不亮,$L_{2}$ 亮,下列分析正确的是 (
A.一定是灯泡 $L_{1}$ 短路
B.一定是灯泡 $L_{1}$ 断路
C.若用测电笔检测 A、B 点都能发光可能是 B 点和零线之间断路
D.若用测电笔检测 A、B 点都能发光可能是 B 点和零线之间短路
C
)A.一定是灯泡 $L_{1}$ 短路
B.一定是灯泡 $L_{1}$ 断路
C.若用测电笔检测 A、B 点都能发光可能是 B 点和零线之间断路
D.若用测电笔检测 A、B 点都能发光可能是 B 点和零线之间短路
答案:
解:家庭电路中各用电器并联,闭合开关$S_{1}$、$S_{2}$后,$L_{2}$亮,说明干路和$L_{2}$所在支路正常。
A选项:若$L_{1}$短路,会造成电源短路,干路电流过大,保险丝熔断或空气开关跳闸,$L_{2}$也不会亮,A错误。
B选项:$L_{1}$不亮可能是断路,也可能是其他原因,“一定”说法过于绝对,B错误。
C选项:测电笔检测A、B点都能发光,说明A、B点均与火线相连。正常情况下,B点接零线,测电笔不发光,若B点和零线之间断路,电流无法通过零线回到电源,B点通过$L_{1}$与火线相连,所以A、B点都能使测电笔发光,C正确。
D选项:若B点和零线之间短路,会造成电源短路,$L_{2}$不亮,D错误。
答案:C
A选项:若$L_{1}$短路,会造成电源短路,干路电流过大,保险丝熔断或空气开关跳闸,$L_{2}$也不会亮,A错误。
B选项:$L_{1}$不亮可能是断路,也可能是其他原因,“一定”说法过于绝对,B错误。
C选项:测电笔检测A、B点都能发光,说明A、B点均与火线相连。正常情况下,B点接零线,测电笔不发光,若B点和零线之间断路,电流无法通过零线回到电源,B点通过$L_{1}$与火线相连,所以A、B点都能使测电笔发光,C正确。
D选项:若B点和零线之间短路,会造成电源短路,$L_{2}$不亮,D错误。
答案:C
9. (2024·淮安)如图甲所示,电源电压保持不变,$R_{1}$ 为定值电阻,滑动变阻器 $R_{2}$ 的最大阻值为 20 Ω.电压表量程为 0~3 V,电流表量程为 0~0.6 A.在保证电路各元件安全的前提下,电压表的示数随滑动变阻器 $R_{2}$ 阻值变化的关系图像如图乙所示.下列说法中正确的是 (
A.电源电压为 7.5 V
B.定值电阻 $R_{1}$ 阻值为 5 Ω
C.电路的最小功率为 0.6 W
D.电流表示数变化范围为0.2A~0.3A
无正确选项(原选项A、B、C均错误)
)A.电源电压为 7.5 V
B.定值电阻 $R_{1}$ 阻值为 5 Ω
C.电路的最小功率为 0.6 W
D.电流表示数变化范围为0.2A~0.3A
答案:
解:由图甲知,$R_1$与$R_2$串联,电压表测$R_1$两端电压,电流表测电路电流。
由图乙知,当$R_{2}=10\Omega$时,$U_{1}=3V$;当$R_{2}' = 20\Omega$时,$U_{1}'=2V$。
根据串联电路特点及欧姆定律,电源电压$U = U_{1}+\frac{U_{1}}{R_{1}}R_{2}=U_{1}'+\frac{U_{1}'}{R_{1}}R_{2}'$。
代入数据:$3V+\frac{3V}{R_{1}}×10\Omega=2V+\frac{2V}{R_{1}}×20\Omega$,解得$R_{1}=10\Omega$。
电源电压$U=3V+\frac{3V}{10\Omega}×10\Omega = 6V$。
电路最小功率:当$R_{2}=20\Omega$时,$I_{\text{min}}=\frac{U}{R_{1}+R_{2}}=\frac{6V}{10\Omega + 20\Omega}=0.2A$,$P_{\text{min}}=UI_{\text{min}}=6V×0.2A = 1.2W$。
综上,无正确选项。
答案:无正确选项(原选项A、B、C均错误)。
由图乙知,当$R_{2}=10\Omega$时,$U_{1}=3V$;当$R_{2}' = 20\Omega$时,$U_{1}'=2V$。
根据串联电路特点及欧姆定律,电源电压$U = U_{1}+\frac{U_{1}}{R_{1}}R_{2}=U_{1}'+\frac{U_{1}'}{R_{1}}R_{2}'$。
代入数据:$3V+\frac{3V}{R_{1}}×10\Omega=2V+\frac{2V}{R_{1}}×20\Omega$,解得$R_{1}=10\Omega$。
电源电压$U=3V+\frac{3V}{10\Omega}×10\Omega = 6V$。
电路最小功率:当$R_{2}=20\Omega$时,$I_{\text{min}}=\frac{U}{R_{1}+R_{2}}=\frac{6V}{10\Omega + 20\Omega}=0.2A$,$P_{\text{min}}=UI_{\text{min}}=6V×0.2A = 1.2W$。
综上,无正确选项。
答案:无正确选项(原选项A、B、C均错误)。
查看更多完整答案,请扫码查看


