《2025年学霸提优大试卷九年级物理上册苏科版》

23.(10分)小明学习了杠杆的平衡条件后,利用如图所示的装置对杠杆做了进一步研究.
(1)杠杆静止时的位置如图甲所示,此时杠杆处于平衡(填“平衡”或“非平衡”)状态.为了使杠杆静止时处于水平位置,接下来的操作是将杠杆的平衡螺母向右端移动.
(2)在杠杆上的B点用如图乙所示的动力F拉杠杆,此时杠杆的类型与B(填序号)相同.
A.天平 B.钓鱼竿 C.钳子
(3)如图丙所示,用弹簧测力计拉杠杆的C点,当弹簧测力计由位置1缓慢转至位置2的过程中,测力计示数变化情况是先变小后变大.
(4)如图丁所示,小明在杠杆左侧距离O点20cm的D处挂一个重为G的物体,在杠杆右侧不同位置处施加竖直向下的力F,保证杠杆处于水平平衡状态,根据多次测量的F、L数据,画出如图戊所示的图像,结合杠杆平衡条件,可求出物重G的大小是2.5N.

答案： 【解析】：
（1）杠杆静止时，就是处于平衡状态；为使杠杆在水平位置平衡，需要使杠杆的重心右移，应将平衡螺母向右调节。
（2）由图乙可知，$OB:OA=2:3$，根据杠杆的平衡条件$F× OB=G× OA$，$F=\frac{OA}{OB}× G=\frac{3}{2}× G$，即此时杠杆是费力杠杆，钓鱼竿就是费力杠杆，天平就是等臂杠杆，钳子是省力杠杆。
（3）图丙中，当弹簧测力计由位置1缓慢转至位置2的过程中，动力臂先变长后变短，而杠杆在水平位置始终保持平衡，根据杠杆平衡条件可知，测力计示数先变小后变大。
（4）设物体重力为G，杠杆上每一格的长度为L，根据杠杆的平衡条件$F_1L_1=F_2L_2$可得，$G× 20cm=F× L$，则$F=\frac{20cm}{L}× G$，由图戊可知当$F=2N$时，$\frac{1}{L}=4m^{-1}$，即$L=\frac{1}{4}m$，则$2N=\frac{20cm}{\frac{1}{4}cm}× G$，$G=2.5N$。
【答案】：
（1）平衡；右；（2）B；（3）先变小后变大；（4）$2.5$。

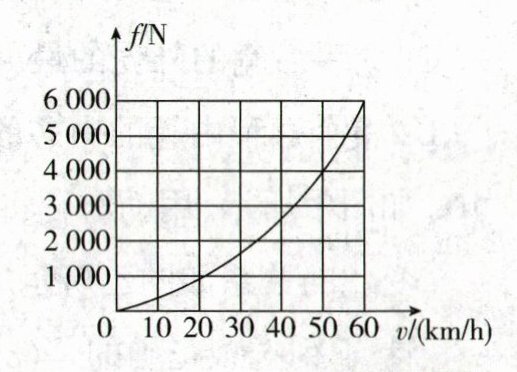
24.(10分)混合动力汽车具有节能、低排放等优点,成为汽车研究与开发领域的重点,某新型混合动力汽车启动时,内燃机不工作,蓄电池向车轮输送能量,当需要高速行驶或蓄电池电能过低时,内燃机启动,既可以向车轮输送能量,又可以给蓄电池充电,车速与所受阻力的关系如图所示.在某次测试中,蓄电池存满电能$7.6×10^{8}\text{J}$,启动时,消耗了20%电能输送给车轮,当汽车速度达到50km/h时,由内燃机提供能量.接下来汽车匀速行驶20km,共消耗燃料14kg,蓄电池充满.已知内燃机效率为40%.(忽略蓄电池和电动机的热损失,$q_{\text{燃料}}= 4.5×10^{7}\text{J/kg}$)求:
(1)汽车匀速行驶时受到的阻力f;
(2)匀速行驶时,汽车牵引力所做的功;
(3)内燃机给车轮供能的效率.

答案：
(1)由图可知，当汽车速度为50km/h时，所受阻力f=4000N。
(2)汽车匀速行驶，牵引力F=f=4000N，行驶距离s=20km=20000m，牵引力所做的功$W=Fs=4000N×20000m=8×10^7J。$
(3)消耗燃料的总能量$Q=mq=14kg×4.5×10^7J/kg=6.3×10^8J，$内燃机输出的有用能量W_有$=Qη=6.3×10^8J×40%=2.52×10^8J。$蓄电池消耗20%电能，需补充的电能W_电$=7.6×10^8J×20%=1.52×10^8J。$内燃机给车轮供能W_轮=W_有 - W_电$=2.52×10^8J - 1.52×10^8J=1×10^9J。$内燃机给车轮供能的效率η_轮=W_轮/W_有$×100%=1×10^9J/2.52×10^8J×100%≈39.68%。$
(1)4000N；$(2)8×10^7J；$
(3)39.68%。