2025年新课堂假期生活暑假生活北京教育出版社七年级数学华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课堂假期生活暑假生活北京教育出版社七年级数学华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 如果等腰三角形的一个内角为$80^{\circ }$,那么它的一个底角为多少度?
答案:
【解析】:本题需要分情况讨论这个$80^{\circ}$的角是底角还是顶角。
情况一:当$80^{\circ}$的角为底角时,满足等腰三角形两底角相等的性质,此时底角就是$80^{\circ}$。
情况二:当$80^{\circ}$的角为顶角时,根据三角形内角和为$180^{\circ}$,且等腰三角形两底角相等,那么底角的度数为$(180^{\circ}-80^{\circ})\div2 = 50^{\circ}$。
【答案】:$80^{\circ}$或$50^{\circ}$
情况一:当$80^{\circ}$的角为底角时,满足等腰三角形两底角相等的性质,此时底角就是$80^{\circ}$。
情况二:当$80^{\circ}$的角为顶角时,根据三角形内角和为$180^{\circ}$,且等腰三角形两底角相等,那么底角的度数为$(180^{\circ}-80^{\circ})\div2 = 50^{\circ}$。
【答案】:$80^{\circ}$或$50^{\circ}$
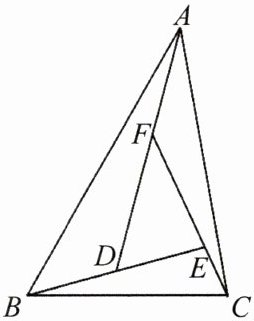
3. 如图,已知$∠BAD = ∠CBE = ∠ACF$,$∠FDE = 60^{\circ }$,$∠DEF = 80^{\circ }$,求$△ABC$各内角的度数.
$∠ABC=$

$∠ABC=$
$60^{\circ}$
,$∠ACB=$$80^{\circ}$
,$∠BAC=$$40^{\circ}$
答案:
【解析】:
- 首先,根据三角形外角性质:
因为$\angle FDE$是$\triangle ABD$的外角,所以$\angle FDE=\angle BAD + \angle ABD$(三角形的一个外角等于与它不相邻的两个内角之和)。
又因为$\angle BAD=\angle CBE$,那么$\angle FDE=\angle CBE+\angle ABD=\angle ABC$。
已知$\angle FDE = 60^{\circ}$,所以$\angle ABC=60^{\circ}$。
然后,同样根据三角形外角性质:
由于$\angle DEF$是$\triangle BCE$的外角,所以$\angle DEF=\angle BCE+\angle CBE$(三角形的一个外角等于与它不相邻的两个内角之和)。
又因为$\angle CBE=\angle ACF$,那么$\angle DEF=\angle ACF+\angle BCE=\angle ACB$。
已知$\angle DEF = 80^{\circ}$,所以$\angle ACB=80^{\circ}$。
最后,根据三角形内角和定理:
在$\triangle ABC$中,$\angle BAC+\angle ABC+\angle ACB = 180^{\circ}$(三角形内角和为$180^{\circ}$)。
把$\angle ABC = 60^{\circ}$,$\angle ACB=80^{\circ}$代入可得:$\angle BAC=180^{\circ}-\angle ABC - \angle ACB$。
即$\angle BAC=180^{\circ}-60^{\circ}-80^{\circ}=40^{\circ}$。
【答案】:$\angle ABC = 60^{\circ}$,$\angle ACB = 80^{\circ}$,$\angle BAC = 40^{\circ}$
- 首先,根据三角形外角性质:
因为$\angle FDE$是$\triangle ABD$的外角,所以$\angle FDE=\angle BAD + \angle ABD$(三角形的一个外角等于与它不相邻的两个内角之和)。
又因为$\angle BAD=\angle CBE$,那么$\angle FDE=\angle CBE+\angle ABD=\angle ABC$。
已知$\angle FDE = 60^{\circ}$,所以$\angle ABC=60^{\circ}$。
然后,同样根据三角形外角性质:
由于$\angle DEF$是$\triangle BCE$的外角,所以$\angle DEF=\angle BCE+\angle CBE$(三角形的一个外角等于与它不相邻的两个内角之和)。
又因为$\angle CBE=\angle ACF$,那么$\angle DEF=\angle ACF+\angle BCE=\angle ACB$。
已知$\angle DEF = 80^{\circ}$,所以$\angle ACB=80^{\circ}$。
最后,根据三角形内角和定理:
在$\triangle ABC$中,$\angle BAC+\angle ABC+\angle ACB = 180^{\circ}$(三角形内角和为$180^{\circ}$)。
把$\angle ABC = 60^{\circ}$,$\angle ACB=80^{\circ}$代入可得:$\angle BAC=180^{\circ}-\angle ABC - \angle ACB$。
即$\angle BAC=180^{\circ}-60^{\circ}-80^{\circ}=40^{\circ}$。
【答案】:$\angle ABC = 60^{\circ}$,$\angle ACB = 80^{\circ}$,$\angle BAC = 40^{\circ}$
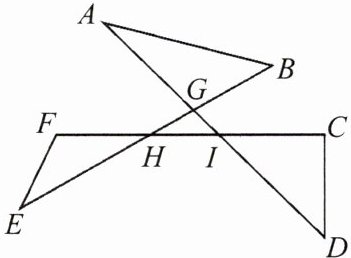
4. 如图,求$∠A + ∠B + ∠C + ∠D + ∠E + ∠F$的度数.

$360^{\circ}$
答案:
【解析】:本题可利用三角形外角的性质,将所求角转化到多边形中,再根据多边形外角和定理求解。
- **步骤一:利用三角形外角性质进行角的转化**
根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABG$中,$\angle AGH=\angle A + \angle B$;
在$\triangle CDI$中,$\angle CID=\angle C + \angle D$;
在$\triangle EFH$中,$\angle FHE=\angle E + \angle F$。
- **步骤二:求$\angle AGH+\angle CID+\angle FHE$的度数**
因为$\angle AGH$、$\angle CID$、$\angle FHE$分别是$\triangle GHI$的外角,
根据多边形外角和定理:多边形的外角和等于$360^{\circ}$,
所以$\angle AGH+\angle CID+\angle FHE = 360^{\circ}$。
- **步骤三:计算$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F$的度数**
由于$\angle AGH=\angle A + \angle B$,$\angle CID=\angle C + \angle D$,$\angle FHE=\angle E + \angle F$,
那么$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F=\angle AGH+\angle CID+\angle FHE = 360^{\circ}$。
【答案】:$360^{\circ}$
- **步骤一:利用三角形外角性质进行角的转化**
根据三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABG$中,$\angle AGH=\angle A + \angle B$;
在$\triangle CDI$中,$\angle CID=\angle C + \angle D$;
在$\triangle EFH$中,$\angle FHE=\angle E + \angle F$。
- **步骤二:求$\angle AGH+\angle CID+\angle FHE$的度数**
因为$\angle AGH$、$\angle CID$、$\angle FHE$分别是$\triangle GHI$的外角,
根据多边形外角和定理:多边形的外角和等于$360^{\circ}$,
所以$\angle AGH+\angle CID+\angle FHE = 360^{\circ}$。
- **步骤三:计算$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F$的度数**
由于$\angle AGH=\angle A + \angle B$,$\angle CID=\angle C + \angle D$,$\angle FHE=\angle E + \angle F$,
那么$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F=\angle AGH+\angle CID+\angle FHE = 360^{\circ}$。
【答案】:$360^{\circ}$
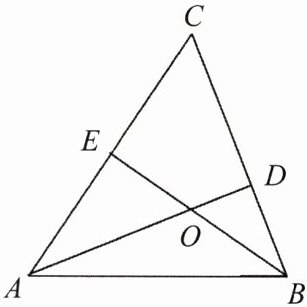
5. 如图,在$△ABC$中,$O$是高$AD$、$BE$的交点,观察图形,试猜想$∠C$和$∠DOE$之间有怎样的数量关系,并说明你的结论的正确性.
猜想:
说明:因为$AD$、$BE$是$\triangle ABC$的高,所以$\angle ADC = \angle BEC = 90^{\circ}$。在四边形$CEOD$中,根据四边形内角和为$360^{\circ}$,可得$\angle C+\angle EOD + \angle ADC+\angle BEC=360^{\circ}$。把$\angle ADC = 90^{\circ}$,$\angle BEC = 90^{\circ}$代入上式得:$\angle C+\angle EOD+90^{\circ}+90^{\circ}=360^{\circ}$,化简可得$\angle C+\angle EOD = 180^{\circ}$,即$\angle C+\angle DOE = 180^{\circ}$。

猜想:
$\angle C+\angle DOE = 180^{\circ}$
说明:因为$AD$、$BE$是$\triangle ABC$的高,所以$\angle ADC = \angle BEC = 90^{\circ}$。在四边形$CEOD$中,根据四边形内角和为$360^{\circ}$,可得$\angle C+\angle EOD + \angle ADC+\angle BEC=360^{\circ}$。把$\angle ADC = 90^{\circ}$,$\angle BEC = 90^{\circ}$代入上式得:$\angle C+\angle EOD+90^{\circ}+90^{\circ}=360^{\circ}$,化简可得$\angle C+\angle EOD = 180^{\circ}$,即$\angle C+\angle DOE = 180^{\circ}$。
答案:
【解析】:
因为$AD$、$BE$是$\triangle ABC$的高,所以$\angle ADC = \angle BEC = 90^{\circ}$。
在四边形$CEOD$中,根据四边形内角和为$360^{\circ}$,可得$\angle C+\angle EOD + \angle ADC+\angle BEC=360^{\circ}$。
把$\angle ADC = 90^{\circ}$,$\angle BEC = 90^{\circ}$代入上式得:$\angle C+\angle EOD+90^{\circ}+90^{\circ}=360^{\circ}$,化简可得$\angle C+\angle EOD = 180^{\circ}$。
【答案】:$\angle C+\angle DOE = 180^{\circ}$
因为$AD$、$BE$是$\triangle ABC$的高,所以$\angle ADC = \angle BEC = 90^{\circ}$。
在四边形$CEOD$中,根据四边形内角和为$360^{\circ}$,可得$\angle C+\angle EOD + \angle ADC+\angle BEC=360^{\circ}$。
把$\angle ADC = 90^{\circ}$,$\angle BEC = 90^{\circ}$代入上式得:$\angle C+\angle EOD+90^{\circ}+90^{\circ}=360^{\circ}$,化简可得$\angle C+\angle EOD = 180^{\circ}$。
【答案】:$\angle C+\angle DOE = 180^{\circ}$
查看更多完整答案,请扫码查看


