《2025年新课堂假期生活暑假生活北京教育出版社七年级数学华师大版》

1. 分别解不等式 $ 2 x - 3 \leq 5 ( x - 3 ) $和 $ \frac { y - 1 } { 6 } - \frac { y + 1 } { 3 } ＞ 1 $，并比较 x、y 的大小。

答案： 【解析】：
1. 解不等式$2x - 3\leqslant5(x - 3)$：
去括号：根据去括号法则$a(b - c)=ab - ac$，可得$2x-3\leqslant5x - 15$。
移项：把含有$x$的项移到一边，常数项移到另一边，得到$2x - 5x\leqslant - 15 + 3$。
合并同类项：$2x-5x=(2 - 5)x=-3x$，$-15 + 3=-12$，则$-3x\leqslant - 12$。
系数化为$1$：不等式两边同时除以$-3$，根据不等式性质，不等式两边同时除以一个负数，不等号方向改变，所以$x\geqslant4$。
2. 解不等式$\frac{y - 1}{6}-\frac{y + 1}{3}\gt1$：
去分母：不等式两边同时乘以$6$，得到$6\times\frac{y - 1}{6}-6\times\frac{y + 1}{3}\gt6\times1$，即$y - 1-2(y + 1)\gt6$。
去括号：根据去括号法则$a(b + c)=ab+ac$，可得$y - 1-2y - 2\gt6$。
移项：把含有$y$的项移到一边，常数项移到另一边，得到$y-2y\gt6 + 1+2$。
合并同类项：$y - 2y=(1 - 2)y=-y$，$6 + 1+2 = 9$，则$-y\gt9$。
系数化为$1$：不等式两边同时除以$-1$，根据不等式性质，不等式两边同时除以一个负数，不等号方向改变，所以$y\lt - 9$。
3. 比较$x$、$y$的大小：
因为$x\geqslant4$，$y\lt - 9$，所以$x\gt y$。
【答案】：解不等式$2x - 3\leqslant5(x - 3)$得$x\geqslant4$；解不等式$\frac{y - 1}{6}-\frac{y + 1}{3}\gt1$得$y\lt - 9$；$x\gt y$。

2. 求不等式组 $ - 2 \leq 3 x - 11 ＜ 4 $的整数解。

答案： 【解析】：本题可将不等式组$-2\leq3x - 11\lt4$拆分成两个不等式$-2\leq3x - 11$和$3x - 11\lt4$，分别求解这两个不等式。
解不等式$-2\leq3x - 11$，移项可得$3x\geq - 2 + 11$，即$3x\geq9$，两边同时除以$3$，解得$x\geq3$。
解不等式$3x - 11\lt4$，移项可得$3x\lt4 + 11$，即$3x\lt15$，两边同时除以$3$，解得$x\lt5$。
综合两个不等式的解，可得不等式组的解集为$3\leq x\lt5$，在这个范围内的整数为$3$和$4$。
【答案】：$3$，$4$

3. 一个工程队规定要在 6 天内完成 300 土方的工程，第一天完成了 60 土方，现在要比原计划至少提前两天完成，则以后平均每天至少要比原计划多完成多少土方？

答案： 【解析】：本题可先求出原计划每天完成的土方数，再根据现在要比原计划至少提前两天完成，计算出剩余天数和剩余土方数，进而求出以后平均每天至少要完成的土方数，最后求出以后平均每天至少要比原计划多完成的土方数。
- **步骤一：计算原计划每天完成的土方数**
已知工程队要在$6$天内完成$300$土方的工程，根据“工作效率$=$工作总量$\div$工作时间”，可得原计划每天完成的土方数为：$300\div6 = 50$（土方）
- **步骤二：计算剩余天数和剩余土方数**
因为第一天已经完成了$60$土方，所以还剩下的土方数为：$300 - 60 = 240$（土方）
原计划是$6$天完成，现在要比原计划至少提前两天完成，即最多用$6 - 2 = 4$天完成，而第一天已经用掉了$1$天，所以剩下的工程需要在$4 - 1 = 3$天内完成。
- **步骤三：计算以后平均每天至少要完成的土方数**
根据“工作效率$=$工作总量$\div$工作时间”，可得以后平均每天至少要完成的土方数为：$240\div3 = 80$（土方）
- **步骤四：计算以后平均每天至少要比原计划多完成的土方数**
用以后平均每天至少要完成的土方数减去原计划每天完成的土方数，可得以后平均每天至少要比原计划多完成的土方数为：$80 - 50 = 30$（土方）
【答案】：$30$

4. 如图是象棋盘的一部分，给每个棋盘格规定不同的数。一个棋子“象”从点 A 出发向点 B 行进（规定：象只能走“田”字格），会有两种不同的路线。

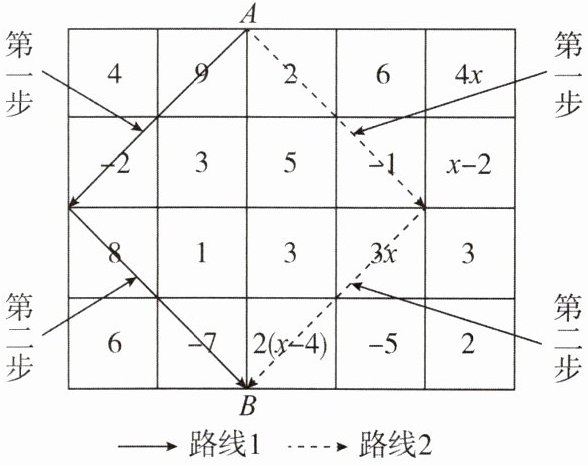
（1）求“路线 1”中第一步和第二步上数字的和；12
（2）若“路线 2”中第一步上两个数字的积大于第二步上两个式子的和，求 x 的取值范围。x＞-8/3

答案： 【解析】：
（1）“路线1”中第一步数字是$4$，第二步数字是$8$，它们的和为$4 + 8 = 12$。
（2）“路线2”中第一步两个数字的积为$2\times4x = 8x$，第二步两个式子的和为$2(x - 4)+3x = 2x-8 + 3x=5x - 8$。
因为第一步上两个数字的积大于第二步上两个式子的和，所以$8x＞5x - 8$，
移项可得$8x-5x＞-8$，
即$3x＞-8$，
解得$x＞-\frac{8}{3}$。
【答案】：
（1）$12$
（2）$x＞-\frac{8}{3}$