《2025年新课堂假期生活暑假生活北京教育出版社七年级数学华师大版》

1. 某校今年秋季七年级和八年级招生总数为500人，计划明年秋季七年级招生数增加20%，八年级招生数增加15%，这样，明年将比今年招生总数增加18%. 求明年秋季七年级、八年级计划招生数.

答案： 【解析】：设今年秋季七年级招生$x$人，八年级招生$y$人。根据今年秋季七年级和八年级招生总数为$500$人，可列方程$x + y = 500$；明年秋季七年级招生数增加$20\%$，即为$(1 + 20\%)x$，八年级招生数增加$15\%$，即为$(1 + 15\%)y$，明年将比今年招生总数增加$18\%$，今年总数是$500$人，那么明年总数是$500\times(1 + 18\%)$，可列方程$(1 + 20\%)x+(1 + 15\%)y = 500\times(1 + 18\%)$。联立方程组$\begin{cases}x + y = 500\\(1 + 20\%)x+(1 + 15\%)y = 500\times(1 + 18\%)\end{cases}$，由$x + y = 500$可得$y = 500 - x$，将其代入$(1 + 20\%)x+(1 + 15\%)y = 500\times(1 + 18\%)$中，得到$1.2x+1.15\times(500 - x)=500\times1.18$，展开式子$1.2x + 575-1.15x = 590$，移项可得$1.2x-1.15x = 590 - 575$，即$0.05x = 15$，解得$x = 300$，把$x = 300$代入$y = 500 - x$，得$y = 500 - 300 = 200$。所以明年七年级计划招生数为$(1 + 20\%)\times300 = 360$人，明年八年级计划招生数为$(1 + 15\%)\times200 = 230$人。
【答案】：七年级360人，八年级230人

2. 运往某地两批化肥，第一批360吨，需用6节火车皮加上15辆汽车；第二批440吨，需用8节火车皮加上10辆汽车. 每节火车皮与每辆汽车平均各装多少吨？

答案： 【解析】：设每节火车皮平均装$x$吨，每辆汽车平均装$y$吨。根据第一批$360$吨，需用$6$节火车皮加上$15$辆汽车，可列方程$6x + 15y = 360$；根据第二批$440$吨，需用$8$节火车皮加上$10$辆汽车，可列方程$8x + 10y = 440$。将第一个方程两边同时除以$3$得到$2x + 5y = 120$，变形为$5y = 120 - 2x$，即$y=\frac{120 - 2x}{5}$。把$y=\frac{120 - 2x}{5}$代入$8x + 10y = 440$中，得到$8x+10\times\frac{120 - 2x}{5}=440$，$8x + 2\times(120 - 2x)=440$，$8x+240 - 4x = 440$，$4x=440 - 240$，$4x = 200$，解得$x = 50$。把$x = 50$代入$y=\frac{120 - 2x}{5}$，$y=\frac{120-2\times50}{5}=\frac{120 - 100}{5}=\frac{20}{5}=4$。
【答案】：每节火车皮平均装$50$吨，每辆汽车平均装$4$吨。

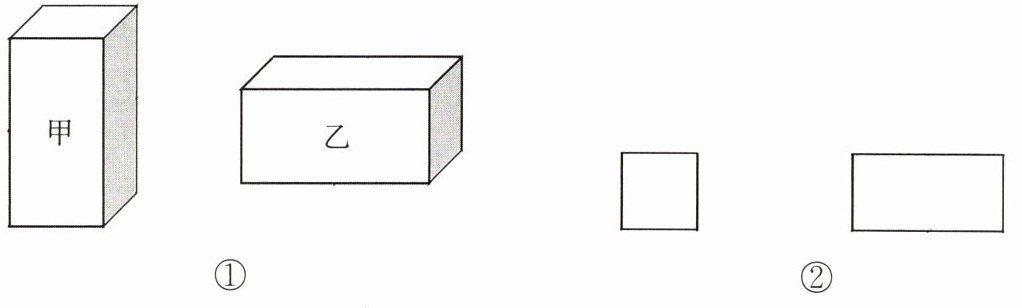
3. 某纸品加工厂为了制作甲、乙两种无盖的长方体小盒（图①），利用边角料裁成正方形和长方形两种硬纸片，长方形的宽和正方形边长相等（图②），现将150张正方形纸片和300张长方形纸片全部用于制作这种小盒，求可做成甲种小盒30个，乙种小盒60个.

答案： 【解析】：设可做成甲种小盒$x$个，乙种小盒$y$个。
制作甲种小盒需要$1$个正方形纸片和$4$个长方形纸片，制作乙种小盒需要$2$个正方形纸片和$3$个长方形纸片。
根据正方形纸片总数为$150$张，可列方程$x + 2y=150$；根据长方形纸片总数为$300$张，可列方程$4x + 3y=300$。
将第一个方程$x + 2y=150$变形为$x=150 - 2y$，代入第二个方程$4x + 3y=300$中，得到$4(150 - 2y)+3y=300$，
即$600-8y + 3y=300$，
$-5y=300 - 600$，
$-5y=-300$，
解得$y = 60$。
把$y = 60$代入$x=150 - 2y$，得$x=150-2×60=150 - 120 = 30$。
【答案】：可做成甲种小盒$30$个，乙种小盒$60$个。