《2025年暑假乐园海南出版社八年级数学人教版》

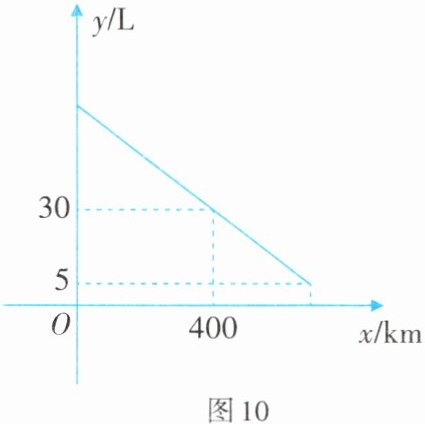
1. 一辆汽车行驶时的耗油量为$0.1\mathrm{L}/\mathrm{k}\mathrm{m}$，如图10是油箱剩余油量$y$(单位：$\mathrm{L}$)关于加满油后已行驶的路程$x$(单位：$\mathrm{k}\mathrm{m}$)的函数图象.
(1)根据图象，直接写出汽车行驶$400\mathrm{k}\mathrm{m}$时油箱内的剩余油量，并计算加满油时油箱的油量；
(2)求$y$关于$x$的函数关系式，并计算该汽车在剩余$5\mathrm{L}$油时已行驶的路程.

答案： 【解析】：
### $(1)$计算汽车行驶$400km$时油箱内的剩余油量和加满油时油箱的油量
由图象可知，汽车行驶$400km$时油箱内的剩余油量为$30L$。
已知汽车行驶时的耗油量为$0.1L/km$，那么行驶$400km$的耗油量为$400\times0.1 = 40L$。
所以加满油时油箱的油量为$40 + 30=70L$。
### $(2)$求$y$关于$x$的函数关系式并计算剩余$5L$油时已行驶的路程
设$y$关于$x$的函数关系式为$y = kx + b$（$k\neq0$）。
把$(0,70)$（加满油时，$x = 0$，$y = 70$）和$(400,30)$代入$y = kx + b$中，可得$\begin{cases}b = 70\\400k + b = 30\end{cases}$。
将$b = 70$代入$400k + b = 30$，得$400k+70 = 30$，解得$k=-0.1$。
所以$y$关于$x$的函数关系式为$y=-0.1x + 70$。
当$y = 5$时，$5=-0.1x + 70$，移项可得$0.1x = 70 - 5$，即$0.1x = 65$，解得$x = 650$。
【答案】：
$(1)$汽车行驶$400km$时油箱内的剩余油量为$\boldsymbol{30L}$，加满油时油箱的油量为$\boldsymbol{70L}$。
$(2)$$y$关于$x$的函数关系式为$\boldsymbol{y = - 0.1x + 70}$，该汽车在剩余$5L$油时已行驶的路程为$\boldsymbol{650km}$。

2. 某产品每件的成本价为$10$元，试销阶段每件产品的销售价$x$(单位：元)与产品的日销售量$y$(单位：件)之间的关系如下表：
|$x$/元|15|20|25|…|
|----|----|----|----|----|
|$y$/件|25|20|15|…|
若$y$是$x$的一次函数.
(1)求$y$与$x$之间的函数关系式；
(2)当每件产品的销售价定为$30$元时，求每日的销售利润.

答案： 【解析】：
(1)设$y$与$x$之间的函数关系式为$y = kx + b$（$k\neq0$）。
把$x = 15$，$y = 25$和$x = 20$，$y = 20$分别代入$y = kx + b$中，可得方程组$\begin{cases}15k + b = 25\\20k + b = 20\end{cases}$。
用第二个方程$20k + b = 20$减去第一个方程$15k + b = 25$，可得：
$(20k + b)-(15k + b)=20 - 25$
$20k + b - 15k - b=-5$
$5k=-5$
解得$k = - 1$。
把$k = - 1$代入$15k + b = 25$，得$15\times(-1)+b = 25$，即$-15 + b = 25$，解得$b = 40$。
所以$y$与$x$之间的函数关系式为$y=-x + 40$。
(2)已知每件产品的成本价为$10$元，当销售价$x = 30$元时，根据$y=-x + 40$，可得日销售量$y=-30 + 40 = 10$件。
根据“利润$=$（售价$-$成本价）$\times$销售量”，则每日的销售利润为$(30 - 10)\times10=20\times10 = 200$元。
【答案】：
(1)$y=-x + 40$；
(2)$200$元