《2025年暑假乐园海南出版社八年级数学人教版》

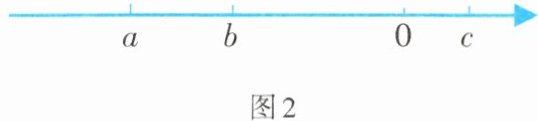
2. 若实数$a$，$b$，$c$在数轴上的对应点如图2所示，试化简：
$\sqrt{a^{2}}-\sqrt{(a + b)^{2}}+\vert b + c\vert+\vert a - c\vert$.

答案： 【解析】：
由数轴可知$a\lt0$，$a + b\lt0$，$b + c\lt0$，$a - c\lt0$。
根据二次根式性质$\sqrt{x^{2}}=\vert x\vert=\begin{cases}x(x\geq0)\\-x(x\lt0)\end{cases}$以及绝对值性质$\vert x\vert=\begin{cases}x(x\geq0)\\-x(x\lt0)\end{cases}$进行化简：
$\sqrt{a^{2}}=\vert a\vert=-a$；
$\sqrt{(a + b)^{2}}=\vert a + b\vert=-(a + b)$；
$\vert b + c\vert=-(b + c)$；
$\vert a - c\vert=-(a - c)$。
将上述化简结果代入原式可得：
$\begin{aligned}&\sqrt{a^{2}}-\sqrt{(a + b)^{2}}+\vert b + c\vert+\vert a - c\vert\\=&-a-(-(a + b))+(-(b + c))+(-(a - c))\\=&-a+(a + b)-(b + c)-(a - c)\\=&-a+a + b - b - c - a + c\\=&-a\end{aligned}$
【答案】：$-a$

3. 已知$y = \sqrt{5 - x}+\sqrt{x - 5}+9$，求$\vert y - 2x\vert-\sqrt[3]{y^{2}-2y + 1}-\sqrt{5xy}$的值.

答案： 【解析】：
本题可先根据二次根式有意义的条件求出$x$的值，再代入求出$y$的值，最后将$x$、$y$的值代入所求式子进行计算。
- **步骤一：根据二次根式有意义的条件求出$x$的值**
要使二次根式$\sqrt{a}$有意义，则被开方数$a\geqslant0$。
在$y = \sqrt{5 - x}+\sqrt{x - 5}+9$中，$\sqrt{5 - x}$有意义，则$5 - x\geqslant0$，即$x\leqslant5$；$\sqrt{x - 5}$有意义，则$x - 5\geqslant0$，即$x\geqslant5$。
要同时满足这两个条件，则$x$只能取$5$。
- **步骤二：将$x = 5$代入$y = \sqrt{5 - x}+\sqrt{x - 5}+9$，求出$y$的值**
把$x = 5$代入$y = \sqrt{5 - x}+\sqrt{x - 5}+9$可得：
$y = \sqrt{5 - 5}+\sqrt{5 - 5}+9=0 + 0 + 9 = 9$
- **步骤三：将$x = 5$，$y = 9$代入$\vert y - 2x\vert-\sqrt[3]{y^{2}-2y + 1}-\sqrt{5xy}$进行计算**
计算$\vert y - 2x\vert$：
把$x = 5$，$y = 9$代入$\vert y - 2x\vert$可得：
$\vert 9 - 2\times5\vert=\vert 9 - 10\vert=\vert -1\vert = 1$
计算$\sqrt[3]{y^{2}-2y + 1}$：
先对$y^{2}-2y + 1$进行因式分解，根据完全平方公式$a^2-2ab+b^2=(a-b)^2$可得$y^{2}-2y + 1=(y - 1)^2$。
把$y = 9$代入$\sqrt[3]{y^{2}-2y + 1}=\sqrt[3]{(y - 1)^2}$可得：
$\sqrt[3]{(9 - 1)^2}=\sqrt[3]{8^2}=\sqrt[3]{64} = 4$
计算$\sqrt{5xy}$：
把$x = 5$，$y = 9$代入$\sqrt{5xy}$可得：
$\sqrt{5\times5\times9}=\sqrt{25\times9}=\sqrt{225} = 15$
计算$\vert y - 2x\vert-\sqrt[3]{y^{2}-2y + 1}-\sqrt{5xy}$的值：
把$\vert y - 2x\vert = 1$，$\sqrt[3]{y^{2}-2y + 1}= 4$，$\sqrt{5xy}= 15$代入$\vert y - 2x\vert-\sqrt[3]{y^{2}-2y + 1}-\sqrt{5xy}$可得：
$1 - 4 - 15=-3 - 15=-18$
【答案】：$-18$

4. 已知三角形的三个顶点坐标分别为$A(3\sqrt{3},0)$，$B(6\sqrt{3},0)$，$C(3\sqrt{3},\sqrt{6})$，求$\triangle ABC$的面积.

答案： 【解析】：本题可根据三角形三个顶点的坐标，判断出三角形的底和高，再根据三角形面积公式求解。
- **步骤一：判断$\triangle ABC$的底和高**
已知$A(3\sqrt{3},0)$，$B(6\sqrt{3},0)$，$C(3\sqrt{3},\sqrt{6})$。
由于$A$、$B$两点的纵坐标都为$0$，说明$A$、$B$两点都在$x$轴上，那么线段$AB$的长度就为$A$、$B$两点横坐标差的绝对值，即$\vert AB\vert=\vert 6\sqrt{3}-3\sqrt{3}\vert = 3\sqrt{3}$，所以$\triangle ABC$的底为$AB = 3\sqrt{3}$。
又因为$A$、$C$两点的横坐标相同，都为$3\sqrt{3}$，说明$AC$垂直于$x$轴，那么$C$点到$x$轴的距离就是$C$点纵坐标的绝对值，即$\vert\sqrt{6}\vert=\sqrt{6}$，所以$\triangle ABC$的高为$\sqrt{6}$。
- **步骤二：根据三角形面积公式计算$\triangle ABC$的面积**
三角形的面积公式为$S = \frac{1}{2}ah$（其中$S$表示面积，$a$表示底，$h$表示高）。
将$a = 3\sqrt{3}$，$h = \sqrt{6}$代入公式可得：
$S_{\triangle ABC}=\frac{1}{2}\times 3\sqrt{3}\times\sqrt{6}=\frac{1}{2}\times 3\sqrt{3\times 6}=\frac{1}{2}\times 3\sqrt{18}=\frac{1}{2}\times 3\times 3\sqrt{2}=\frac{9\sqrt{2}}{2}$
【答案】：$\frac{9\sqrt{2}}{2}$