第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
2. 阅读与思考:下面是一名同学的数学学习笔记,请仔细阅读并完成相应任务.
瓦里尼翁平行四边形
我们知道,如图18,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA,的中点,顺次连接E,F,G,H,得到的四边形EFGH是平行四边形.
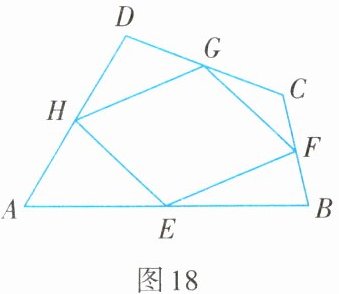
我查阅了许多资料,得知这个平行四边形EFGH被称为瓦里尼翁平行四边形.瓦里尼翁(Varingnon,Pierre 1654—1722)是法国数学家、力学家.瓦里尼翁平行四边形与原四边形关系密切.
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形.
②瓦里尼翁平行四边形的周长与原四边形对角线的长度有一定关系.
③瓦里尼翁平行四边形的面积等于原四边形面积的一半.证明如下:
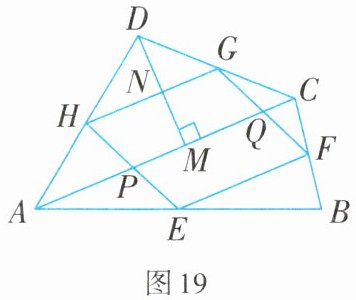
如图19,连接AC,分别交EH,FG于点P,Q,过点D作DM⊥AC于点M,交HG于点N.
∵点H,G分别为AD,CD的中点,∴HG//AC,HG=$\frac{1}{2}$AC.(依据1)
∴$\frac{DN}{NM}=\frac{DG}{GC}$.∵DG=GC,∴DN=NM=$\frac{1}{2}$DM.
∵四边形EFGH是瓦里尼翁平行四边形,∴HE//GF,即HP//GQ.
∵HG//AC,即HG//PQ,
∴四边形HPQG是平行四边形.(依据2)∴$S_{□HPQG}=HG\cdot MN=\frac{1}{2}HG\cdot DM$.
∵$S_{△ADC}=\frac{1}{2}AC\cdot DM=HG\cdot DM$,∴$S_{□HPQG}=\frac{1}{2}S_{△ADC}$.同理,…
任务:
(1)填空:材料中的依据1是指:______________________________,依据2是指:______________________________;
(2)请用刻度尺、三角板等工具,画一个四边形ABCD及它的瓦里尼翁平行四边形EFGH,使得四边形EFGH为矩形;(要求同时画出四边形ABCD的对角线)
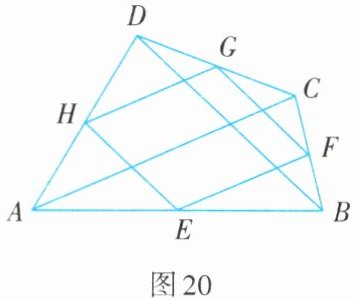
(3)在图18中,分别连接AC,BD得到图20,请猜想瓦里尼翁平行四边形EFGH的周长与对角线AC,BD长度的关系,并证明你的结论.
瓦里尼翁平行四边形
我们知道,如图18,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA,的中点,顺次连接E,F,G,H,得到的四边形EFGH是平行四边形.


我查阅了许多资料,得知这个平行四边形EFGH被称为瓦里尼翁平行四边形.瓦里尼翁(Varingnon,Pierre 1654—1722)是法国数学家、力学家.瓦里尼翁平行四边形与原四边形关系密切.
①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形.
②瓦里尼翁平行四边形的周长与原四边形对角线的长度有一定关系.
③瓦里尼翁平行四边形的面积等于原四边形面积的一半.证明如下:
如图19,连接AC,分别交EH,FG于点P,Q,过点D作DM⊥AC于点M,交HG于点N.
∵点H,G分别为AD,CD的中点,∴HG//AC,HG=$\frac{1}{2}$AC.(依据1)
∴$\frac{DN}{NM}=\frac{DG}{GC}$.∵DG=GC,∴DN=NM=$\frac{1}{2}$DM.
∵四边形EFGH是瓦里尼翁平行四边形,∴HE//GF,即HP//GQ.
∵HG//AC,即HG//PQ,
∴四边形HPQG是平行四边形.(依据2)∴$S_{□HPQG}=HG\cdot MN=\frac{1}{2}HG\cdot DM$.
∵$S_{△ADC}=\frac{1}{2}AC\cdot DM=HG\cdot DM$,∴$S_{□HPQG}=\frac{1}{2}S_{△ADC}$.同理,…
任务:
(1)填空:材料中的依据1是指:______________________________,依据2是指:______________________________;
(2)请用刻度尺、三角板等工具,画一个四边形ABCD及它的瓦里尼翁平行四边形EFGH,使得四边形EFGH为矩形;(要求同时画出四边形ABCD的对角线)
(3)在图18中,分别连接AC,BD得到图20,请猜想瓦里尼翁平行四边形EFGH的周长与对角线AC,BD长度的关系,并证明你的结论.

答案:
【解析】:
(1) 依据1是三角形中位线定理(三角形的中位线平行于第三边,并且等于第三边的一半);依据2是两组对边分别平行的四边形是平行四边形。
(2) 画图步骤:
先用三角板画一条线段$AC$。
再用三角板过$A$,$C$分别作$AC$的垂线$l_1$,$l_2$。
在$l_1$上取一点$B$,$l_2$上取一点$D$,连接$AB$,$BC$,$CD$,$DA$,得到四边形$ABCD$。
分别取$AB$,$BC$,$CD$,$DA$的中点$E$,$F$,$G$,$H$,顺次连接$E$,$F$,$G$,$H$,得到瓦里尼翁平行四边形$EFGH$(此时$EFGH$为矩形,因为原四边形$ABCD$对角线$AC\perp BD$,根据三角形中位线定理可推出$EH\perp HG$,平行四边形$EFGH$有一个角是直角就是矩形)。
(3) 猜想:瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$。
证明:
因为点$E$,$H$分别是$AB$,$AD$的中点,根据三角形中位线定理,所以$EH// BD$,$EH=\frac{1}{2}BD$。
同理,$FG// BD$,$FG = \frac{1}{2}BD$;$EF// AC$,$EF=\frac{1}{2}AC$;$HG// AC$,$HG=\frac{1}{2}AC$。
则四边形$EFGH$的周长为$EH + HG+FG + EF=\frac{1}{2}BD+\frac{1}{2}AC+\frac{1}{2}BD+\frac{1}{2}AC=AC + BD$。
【答案】:
(1) 三角形中位线定理(三角形的中位线平行于第三边,并且等于第三边的一半);两组对边分别平行的四边形是平行四边形。
(2) 按上述步骤画图(略)。
(3) 瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$,证明如上。
(1) 依据1是三角形中位线定理(三角形的中位线平行于第三边,并且等于第三边的一半);依据2是两组对边分别平行的四边形是平行四边形。
(2) 画图步骤:
先用三角板画一条线段$AC$。
再用三角板过$A$,$C$分别作$AC$的垂线$l_1$,$l_2$。
在$l_1$上取一点$B$,$l_2$上取一点$D$,连接$AB$,$BC$,$CD$,$DA$,得到四边形$ABCD$。
分别取$AB$,$BC$,$CD$,$DA$的中点$E$,$F$,$G$,$H$,顺次连接$E$,$F$,$G$,$H$,得到瓦里尼翁平行四边形$EFGH$(此时$EFGH$为矩形,因为原四边形$ABCD$对角线$AC\perp BD$,根据三角形中位线定理可推出$EH\perp HG$,平行四边形$EFGH$有一个角是直角就是矩形)。
(3) 猜想:瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$。
证明:
因为点$E$,$H$分别是$AB$,$AD$的中点,根据三角形中位线定理,所以$EH// BD$,$EH=\frac{1}{2}BD$。
同理,$FG// BD$,$FG = \frac{1}{2}BD$;$EF// AC$,$EF=\frac{1}{2}AC$;$HG// AC$,$HG=\frac{1}{2}AC$。
则四边形$EFGH$的周长为$EH + HG+FG + EF=\frac{1}{2}BD+\frac{1}{2}AC+\frac{1}{2}BD+\frac{1}{2}AC=AC + BD$。
【答案】:
(1) 三角形中位线定理(三角形的中位线平行于第三边,并且等于第三边的一半);两组对边分别平行的四边形是平行四边形。
(2) 按上述步骤画图(略)。
(3) 瓦里尼翁平行四边形$EFGH$的周长等于$AC + BD$,证明如上。
查看更多完整答案,请扫码查看


