《2025年暑假乐园海南出版社八年级数学人教版》

蜘蛛如何吃到苍蝇
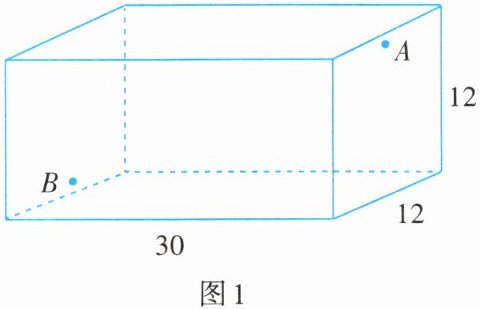
在一个如图1所示(单位:英尺,1英尺=0.3048米)的长方体房间里,一只蜘蛛在一面墙的中间离天花板1英尺的A处,苍蝇则在对面墙的中间离地板1英尺的B处.苍蝇非常害怕,以至于无法动弹.
问:蜘蛛为了捉住苍蝇需要爬的最短距离是多少?
这道有趣的题目最早出现在1903年的英国报纸上,是19世纪英国知名的谜题创作者亨利·欧内斯特·杜登尼创作的广为人知的谜题之一.你能解决这一谜题吗?你是怎么做的?

答案： 解：蜘蛛可以经天花板从A点爬到B点：30+12=42(英尺)
答：蜘蛛为了捉住苍蝇需要爬的最短距离是42英尺。

1. 计算$3\sqrt {2}-\sqrt {2}$的值是( ).
A. 2
B. 3
C. $\sqrt {2}$
D. $2\sqrt {2}$

答案： 【解析】：本题可根据合并同类二次根式的法则来计算$3\sqrt {2}-\sqrt {2}$的值。
合并同类二次根式的法则是：同类二次根式相加减，把被开方数不变，系数相加减。
在$3\sqrt {2}-\sqrt {2}$中，$3\sqrt {2}$与$\sqrt {2}$是同类二次根式，将它们的系数相减，被开方数不变，可得：
$3\sqrt {2}-\sqrt {2}=(3 - 1)\sqrt {2}=2\sqrt {2}$
【答案】：D