第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
在物理学中有很多公式可以直接或间接看成一次函数. 例如,在弹性限度内,弹簧的长度随着拉力的增大而不断增加,当弹簧所受的外力过大时,会损坏它的弹性,使得弹簧被拉到最长且无法复原. 某班在实践课上对“弹簧的长度与所受外力之间的关系”进行了探究.
(1)方案设计
“智慧小组”在探究弹簧测力计的“弹簧的长度与所受外力之间的关系”时,多次改变砝码的质量x(单位:g),测量得到弹簧的长度y(单位:cm),且通过实验记录得到的数据如表所示:
如图10,“智慧小组”根据实验数据,建立平面直角坐标系,并绘制了部分图象.
(2)问题解决
①材料中的数据表格反映了两个变量之间的关系,其中自变量是______;
②在弹性限度内,求弹簧的长度y与所挂砝码的质量x之间的关系式;当砝码的质量为75g时,求弹簧的长度;
③在不损坏该弹簧的弹性限度的情况下,其所挂砝码的质量应不超过______g;
④根据表格数据,在平面直角坐标系中补全该函数的图象.
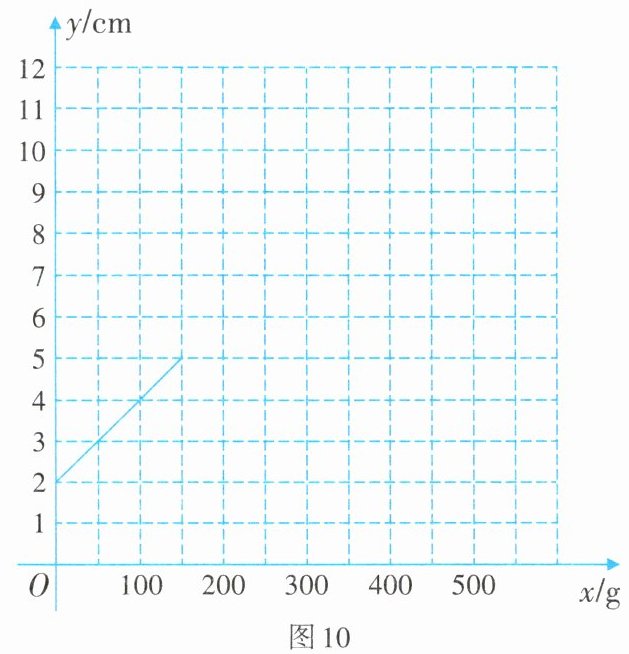
(1)方案设计
“智慧小组”在探究弹簧测力计的“弹簧的长度与所受外力之间的关系”时,多次改变砝码的质量x(单位:g),测量得到弹簧的长度y(单位:cm),且通过实验记录得到的数据如表所示:

如图10,“智慧小组”根据实验数据,建立平面直角坐标系,并绘制了部分图象.
(2)问题解决
①材料中的数据表格反映了两个变量之间的关系,其中自变量是______;
②在弹性限度内,求弹簧的长度y与所挂砝码的质量x之间的关系式;当砝码的质量为75g时,求弹簧的长度;
③在不损坏该弹簧的弹性限度的情况下,其所挂砝码的质量应不超过______g;
④根据表格数据,在平面直角坐标系中补全该函数的图象.

答案:
解:①砝码的质量$x$
②设$y = kx + b$,把$(0,2)$,$(50,3)$代入可得
$\begin{cases}b = 2\\50k + b = 3\end{cases}$,解得$\begin{cases}k=\frac{1}{50}\\b = 2\end{cases}$,
所以$y=\frac{1}{50}x + 2$。
当$x = 75$时,$y=\frac{1}{50}\times75 + 2 = 3.5$,弹簧的长度为3.5cm。
③$275$
④
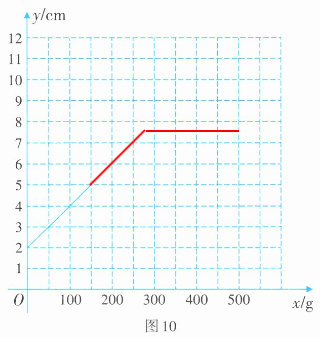
解:①砝码的质量$x$
②设$y = kx + b$,把$(0,2)$,$(50,3)$代入可得
$\begin{cases}b = 2\\50k + b = 3\end{cases}$,解得$\begin{cases}k=\frac{1}{50}\\b = 2\end{cases}$,
所以$y=\frac{1}{50}x + 2$。
当$x = 75$时,$y=\frac{1}{50}\times75 + 2 = 3.5$,弹簧的长度为3.5cm。
③$275$
④

查看更多完整答案,请扫码查看


