《2025年暑假乐园海南出版社八年级数学人教版》

5. 张老师在计算机上画一个长方形，已知长方形的长是$\sqrt { 1 4 0 \pi } \mathrm { cm }$，宽是$\sqrt { 3 5 \pi } \mathrm { cm }$.他还想画一个面积与其相等的圆，请你帮助张老师求出圆的半径.

答案： 【解析】：本题可先根据长方形的长和宽求出长方形的面积，再根据圆的面积公式求出圆的半径。
- **步骤一：计算长方形的面积**
根据长方形的面积公式$S = 长\times宽$，已知长方形的长是$\sqrt { 140\pi } \mathrm { cm }$，宽是$\sqrt { 35\pi } \mathrm { cm }$，则长方形的面积为：
$S_{长方形}=\sqrt { 140\pi }\times\sqrt { 35\pi }$
根据二次根式乘法法则$\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}$（$a\geq0,b\geq0$）对上式进行化简：
$S_{长方形}=\sqrt { 140\pi\times 35\pi }=\sqrt{4900\pi^{2}} = 70\pi(\mathrm{cm}^{2})$
- **步骤二：根据圆的面积公式求出圆的半径**
设圆的半径为$r\mathrm{cm}$，根据圆的面积公式$S = \pi r^{2}$，因为圆的面积与长方形的面积相等，所以可得$\pi r^{2}=70\pi$。
等式两边同时除以$\pi$，得到$r^{2}=70$。
因为$r\gt0$，所以对$r^{2}=70$两边同时开平方，可得$r = \sqrt { 70 }\mathrm{cm}$。
【答案】：$\sqrt { 70 }\mathrm{cm}$

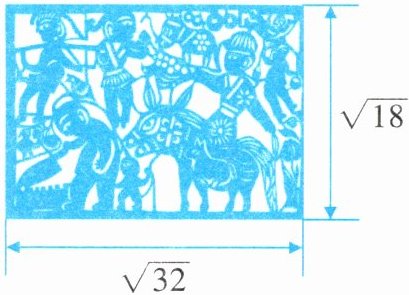
6. 剪纸是一门古老的传统民间艺术，具有明显的地域特色和极高的艺术价值.为传承这一艺术，我市某中学举办剪纸艺术大赛，要求参赛作品的面积在$20 \mathrm { dm } ^ { 2 }$以上.下图是小悦同学的参赛作品(单位：$\mathrm { dm }$).
(1)通过计算，判断小悦的作品是否符合参赛标准；
(2)小涵给小悦提出建议：在参赛作品周围贴上金色彩条，这样参赛作品更漂亮，则需要彩条的长度约为多少？(彩条的宽度忽略不计，结果保留一位小数，参考数据：$\sqrt { 2 } \approx 1.4$)

答案： 【解析】：
(1) 先根据长方形面积公式$S = a\times b$（$a$、$b$为长方形的长和宽）计算作品面积，再与$20\mathrm{dm}^2$比较。
已知作品长$a=\sqrt{32}$，宽$b = \sqrt{18}$，则面积$S=\sqrt{32}\times\sqrt{18}$。
根据二次根式乘法法则$\sqrt{m}\times\sqrt{n}=\sqrt{mn}(m\geq0,n\geq0)$，可得$S=\sqrt{32\times18}=\sqrt{576}=24\mathrm{dm}^2$。
因为$24＞20$，所以小悦的作品符合参赛标准。
(2) 根据长方形周长公式$C = 2(a + b)$计算彩条长度。
$a=\sqrt{32}=4\sqrt{2}$，$b=\sqrt{18}=3\sqrt{2}$，则$C = 2(\sqrt{32}+\sqrt{18})=2(4\sqrt{2}+3\sqrt{2})$。
先合并同类二次根式：$2(4\sqrt{2}+3\sqrt{2})=2\times7\sqrt{2}=14\sqrt{2}$。
把$\sqrt{2}\approx1.4$代入，$14\sqrt{2}\approx14\times1.4 = 19.6\mathrm{dm}$。
【答案】：
(1) 符合参赛标准；
(2) $19.6\mathrm{dm}$。