《2025年暑假乐园海南出版社八年级数学人教版》

2. 下列计算正确的是( ).
A. $\sqrt {12}=2\sqrt {3}$
B. $\sqrt {\frac {3}{2}}=\frac {\sqrt {3}}{2}$
C. $\sqrt {-x^{3}}=-x\sqrt {x}$
D. $\sqrt {x^{2}}=x$

答案： 【解析】：本题可根据二次根式的性质和化简规则，对每个选项逐一进行分析。
- **选项A：判断$\sqrt {12}=2\sqrt {3}$是否正确**
将$12$分解因数可得$12 = 4\times3$，根据二次根式的乘法法则$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}$（$a\geq0,b\geq0$），则$\sqrt{12}=\sqrt{4\times3}=\sqrt{4}\times\sqrt{3}$。
因为$\sqrt{4} = 2$，所以$\sqrt{12}=2\sqrt{3}$，该选项**正确**。
- **选项B：判断$\sqrt {\frac {3}{2}}=\frac {\sqrt {3}}{2}$是否正确**
根据二次根式的除法法则$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$（$a\geq0,b\gt0$），可得$\sqrt{\frac{3}{2}}=\frac{\sqrt{3}}{\sqrt{2}}$。
为了将分母有理化，给分子分母同时乘以$\sqrt{2}$，则$\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3}\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\frac{\sqrt{6}}{2}\neq\frac{\sqrt{3}}{2}$，该选项**错误**。
- **选项C：判断$\sqrt {-x^{3}}=-x\sqrt {x}$是否正确**
要使二次根式$\sqrt{-x^3}$有意义，则$-x^3\geq0$，即$x^3\leq0$，那么$x\leq0$。
$\sqrt{-x^3}=\sqrt{-x\cdot x^2}$，根据二次根式的乘法法则可得$\sqrt{-x\cdot x^2}=\sqrt{x^2}\cdot\sqrt{-x}$。
因为$x\leq0$，所以$\sqrt{x^2} = -x$，则$\sqrt{-x^3}=-x\sqrt{-x}\neq -x\sqrt{x}$，该选项**错误**。
- **选项D：判断$\sqrt {x^{2}}=x$是否正确**
根据二次根式的性质$\sqrt{a^2}=\vert a\vert$，可得$\sqrt{x^2}=\vert x\vert$。
当$x\geq0$时，$\vert x\vert = x$；当$x\lt0$时，$\vert x\vert = -x$，所以$\sqrt{x^2}=\vert x\vert\neq x$，该选项**错误**。
【答案】：A

3. 估计$\sqrt {8}×\sqrt {\frac {1}{2}}+\sqrt {18}$的运算结果应在( ).
A. 5和6之间
B. 6和7之间
C. 7和8之间
D. 8和9之间

答案： 【解析】：本题可先根据二次根式的运算法则对原式进行化简，再估算化简后式子的结果所在的范围。
- **步骤一：化简原式**
根据二次根式乘法法则$\sqrt{a}\times\sqrt{b}=\sqrt{ab}$（$a\geq0,b\geq0$）对$\sqrt{8}\times\sqrt{\frac{1}{2}}$进行化简：
$\sqrt{8}\times\sqrt{\frac{1}{2}}=\sqrt{8\times\frac{1}{2}}=\sqrt{4}=2$
再对$\sqrt{18}$进行化简，将$18$分解因数可得$18 = 9\times2$，根据二次根式的性质$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}$（$a\geq0,b\geq0$）可得：
$\sqrt{18}=\sqrt{9\times2}=\sqrt{9}\times\sqrt{2}=3\sqrt{2}$
将上述化简结果代入原式可得：
$\sqrt{8}\times\sqrt{\frac{1}{2}}+\sqrt{18}=2 + 3\sqrt{2}$
- **步骤二：估算$3\sqrt{2}$的范围**
因为$\sqrt{2}\approx1.414$，所以$3\sqrt{2}\approx3\times1.414 = 4.242$。
也可以通过比较平方数的大小来估算$\sqrt{2}$的范围，因为$1^2 = 1$，$2^2 = 4$，且$1\lt 2\lt 4$，所以$1\lt\sqrt{2}\lt 2$，不等式两边同时乘以$3$可得$3\lt 3\sqrt{2}\lt 6$。
进一步精确估算，因为$1.4^2 = 1.96$，$1.5^2 = 2.25$，且$1.96\lt 2\lt 2.25$，所以$1.4\lt\sqrt{2}\lt 1.5$，不等式两边同时乘以$3$可得$4.2\lt 3\sqrt{2}\lt 4.5$。
- **步骤三：估算$2 + 3\sqrt{2}$的范围**
由$4.2\lt 3\sqrt{2}\lt 4.5$，不等式两边同时加$2$可得$2 + 4.2\lt 2 + 3\sqrt{2}\lt 2 + 4.5$，即$6.2\lt 2 + 3\sqrt{2}\lt 6.5$。
所以$\sqrt{8}\times\sqrt{\frac{1}{2}}+\sqrt{18}$的运算结果在$6$和$7$之间。
【答案】：B

4. 下列根式中,不能与$\sqrt {48}$合并的是( ).
A. $\sqrt {0.12}$
B. $\sqrt {18}$
C. $\sqrt {1\frac {1}{3}}$
D. $-\sqrt {75}$

答案： 【解析】：本题可先将$\sqrt{48}$以及各选项中的根式化为最简二次根式，再根据同类二次根式的定义判断哪些根式能与$\sqrt{48}$合并。
- **步骤一：将$\sqrt{48}$化为最简二次根式**
根据二次根式的性质$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}$（$a\geq0,b\geq0$）对$\sqrt{48}$进行化简：
$\sqrt{48}=\sqrt{16\times3}=\sqrt{16}\times\sqrt{3}=4\sqrt{3}$
- **步骤二：分别将各选项中的根式化为最简二次根式**
**选项A：$\sqrt{0.12}$**
将$0.12$化为分数$\frac{12}{100}$，则$\sqrt{0.12}=\sqrt{\frac{12}{100}}=\frac{\sqrt{12}}{\sqrt{100}}=\frac{\sqrt{4\times3}}{10}=\frac{2\sqrt{3}}{10}=\frac{\sqrt{3}}{5}$。
**选项B：$\sqrt{18}$**
同样根据二次根式的性质对$\sqrt{18}$进行化简：
$\sqrt{18}=\sqrt{9\times2}=\sqrt{9}\times\sqrt{2}=3\sqrt{2}$
**选项C：$\sqrt{1\frac{1}{3}}$**
先将带分数$1\frac{1}{3}$化为假分数$\frac{4}{3}$，再进行化简：
$\sqrt{1\frac{1}{3}}=\sqrt{\frac{4}{3}}=\frac{\sqrt{4}}{\sqrt{3}}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}$
**选项D：$-\sqrt{75}$**
对$-\sqrt{75}$进行化简：
$-\sqrt{75}=-\sqrt{25\times3}=-\sqrt{25}\times\sqrt{3}=-5\sqrt{3}$
- **步骤三：根据同类二次根式的定义判断哪些根式能与$\sqrt{48}$合并**
几个二次根式化成最简二次根式后，如果被开方数相同，这几个二次根式叫做同类二次根式，同类二次根式可以合并。
因为$\sqrt{48}=4\sqrt{3}$，选项A、C、D化简后被开方数都是$3$，与$\sqrt{48}$是同类二次根式，可以合并；而选项B化简后为$3\sqrt{2}$，被开方数是$2$，与$\sqrt{48}$不是同类二次根式，不能合并。
【答案】：B

5. 已知$a-b=2\sqrt {3}-1,ab=\sqrt {3}$,则$(a+1)(b-1)$的值为( ).
A. $-\sqrt {3}$
B. $3\sqrt {3}$
C. $3\sqrt {2}-2$
D. $\sqrt {3}-1$

答案： 【解析】：本题可先将$(a + 1)(b - 1)$展开，然后将$a - b$与$ab$的值代入展开式进行计算。
- **步骤一：展开$(a + 1)(b - 1)$**
根据多项式乘法法则$(m+n)(p-q)=mp-mq+np-nq$，将$(a + 1)(b - 1)$展开可得：
$(a + 1)(b - 1)=ab - a + b - 1=ab-(a - b)-1$
- **步骤二：代入$a - b$与$ab$的值进行计算**
已知$a - b = 2\sqrt {3} - 1$，$ab = \sqrt {3}$，将其代入上式可得：
$(a + 1)(b - 1)=\sqrt{3}-(2\sqrt{3}-1)-1$
去括号：$\sqrt{3}-(2\sqrt{3}-1)-1=\sqrt{3}-2\sqrt{3}+1 - 1$
合并同类项：$\sqrt{3}-2\sqrt{3}+1 - 1=(\sqrt{3}-2\sqrt{3})+(1 - 1)=-\sqrt{3}+0=-\sqrt{3}$
【答案】：A

6. 下列运算中,错误的是( ).
A. $\sqrt {2}×\sqrt {3}=\sqrt {6}$
B. $2\sqrt {2}+3\sqrt {2}=5\sqrt {2}$
C. $\frac {1}{\sqrt {2}}=\frac {\sqrt {2}}{2}$
D. $\sqrt {(\sqrt {2}-\sqrt {3})^{2}}=\sqrt {2}-\sqrt {3}$

答案： 【解析】：本题可根据二次根式的运算法则，逐一分析选项。
- **选项A：判断$\sqrt {2}×\sqrt {3}=\sqrt {6}$是否正确**
根据二次根式乘法法则：$\sqrt{a}\times\sqrt{b}=\sqrt{ab}$（$a\geq0,b\geq0$），可得$\sqrt{2}\times\sqrt{3}=\sqrt{2\times3}=\sqrt{6}$，所以该选项**正确**。
- **选项B：判断$2\sqrt {2}+3\sqrt {2}=5\sqrt {2}$是否正确**
二次根式的加减运算，实质是合并同类二次根式，同类二次根式是指几个二次根式化成最简二次根式后，如果被开方数相同，这几个二次根式叫做同类二次根式。
$2\sqrt{2}$与$3\sqrt{2}$是同类二次根式，可将系数相加，根式部分不变，即$2\sqrt{2}+3\sqrt{2}=(2 + 3)\sqrt{2}=5\sqrt{2}$，所以该选项**正确**。
- **选项C：判断$\frac {1}{\sqrt {2}}=\frac {\sqrt {2}}{2}$是否正确**
分母有理化是指通过一些方法将分母中的根号去掉。对于$\frac{1}{\sqrt{2}}$，给分子分母同时乘以$\sqrt{2}$，可得$\frac{1\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}=\frac{\sqrt{2}}{2}$，所以该选项**正确**。
- **选项D：判断$\sqrt {(\sqrt {2}-\sqrt {3})^{2}}=\sqrt {2}-\sqrt {3}$是否正确**
根据二次根式的性质$\sqrt{a^2}=\vert a\vert$，可得$\sqrt{(\sqrt{2}-\sqrt{3})^2}=\vert\sqrt{2}-\sqrt{3}\vert$。
因为$\sqrt{2}\lt\sqrt{3}$，所以$\sqrt{2}-\sqrt{3}\lt0$。
根据绝对值的性质，当$a\lt0$时，$\vert a\vert=-a$，则$\vert\sqrt{2}-\sqrt{3}\vert=-(\sqrt{2}-\sqrt{3})=\sqrt{3}-\sqrt{2}\neq\sqrt{2}-\sqrt{3}$，所以该选项**错误**。
【答案】：D

7. 化简$\sqrt {3}-\sqrt {3}(1-\sqrt {3})$的结果是( ).
A. 3
B. -3
C. $\sqrt {3}$
D. $-\sqrt {3}$

答案： 【解析】：本题可先根据乘法分配律去括号，再进行二次根式的加减运算。
- **步骤一：根据乘法分配律去括号**
乘法分配律是指两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。用字母表示为$(a+b)\times c=a\times c+b\times c$。
在$\sqrt {3}-\sqrt {3}(1 - \sqrt {3})$中，$a = 1$，$b = -\sqrt{3}$，$c = \sqrt{3}$，根据乘法分配律可得：
$\sqrt {3}-\sqrt {3}(1 - \sqrt {3})=\sqrt {3}-(\sqrt {3}\times1 - \sqrt {3}\times\sqrt {3})=\sqrt {3}-(\sqrt {3} - 3)$
去括号法则为：括号前是“$-$”，把括号和它前面的“$-$”去掉后，原括号里各项的符号都要改变。
所以$\sqrt {3}-(\sqrt {3} - 3)=\sqrt {3}-\sqrt {3} + 3$。
- **步骤二：进行二次根式的加减运算**
二次根式相加减，先把各个二次根式化成最简二次根式，再把被开方数相同的二次根式进行合并，合并方法为系数相加减，根式不变。
在$\sqrt {3}-\sqrt {3} + 3$中，$\sqrt{3}$与$-\sqrt{3}$是同类二次根式，将它们合并可得：
$\sqrt {3}-\sqrt {3} + 3=(\sqrt {3}-\sqrt {3}) + 3=0 + 3 = 3$
【答案】：A

8. 下列运算中,错误的是( ).
A. $\sqrt {24}=2\sqrt {6}$
B. $\sqrt {\frac {1}{3}}=\frac {\sqrt {3}}{3}$
C. $\frac {\sqrt {2}}{\sqrt {3}}=\frac {\sqrt {6}}{3}$
D. $\frac {1}{\sqrt {2}+\sqrt {3}}=\sqrt {2}-\sqrt {3}$

答案： 【解析】：本题可根据二次根式的化简规则和分母有理化的方法，对各选项逐一进行分析。
- **选项A：化简$\sqrt{24}$**
根据二次根式的性质$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}$（$a\geq0,b\geq0$），对$\sqrt{24}$进行化简：
$\sqrt{24}=\sqrt{4\times6}=\sqrt{4}\times\sqrt{6}=2\sqrt{6}$
所以该选项**正确**。
- **选项B：化简$\sqrt{\frac{1}{3}}$**
根据二次根式的性质$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$（$a\geq0,b\gt0$），对$\sqrt{\frac{1}{3}}$进行化简：
$\sqrt{\frac{1}{3}}=\frac{\sqrt{1}}{\sqrt{3}}=\frac{1}{\sqrt{3}}$
为了将分母有理化，给分子分母同时乘以$\sqrt{3}$，得到：
$\frac{1\times\sqrt{3}}{\sqrt{3}\times\sqrt{3}}=\frac{\sqrt{3}}{3}$
所以该选项**正确**。
- **选项C：化简$\frac{\sqrt{2}}{\sqrt{3}}$**
为了将分母有理化，给分子分母同时乘以$\sqrt{3}$，得到：
$\frac{\sqrt{2}\times\sqrt{3}}{\sqrt{3}\times\sqrt{3}}=\frac{\sqrt{6}}{3}$
所以该选项**正确**。
- **选项D：化简$\frac{1}{\sqrt{2}+\sqrt{3}}$**
为了将分母有理化，给分子分母同时乘以$\sqrt{3}-\sqrt{2}$，得到：
$\begin{aligned}\frac{1}{\sqrt{2}+\sqrt{3}}&=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{2}+\sqrt{3})(\sqrt{3}-\sqrt{2})}\\&=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^2-(\sqrt{2})^2}\\&=\frac{\sqrt{3}-\sqrt{2}}{3 - 2}\\&=\sqrt{3}-\sqrt{2}\end{aligned}$
而该选项结果为$\sqrt{2}-\sqrt{3}$，所以该选项**错误**。
【答案】：D

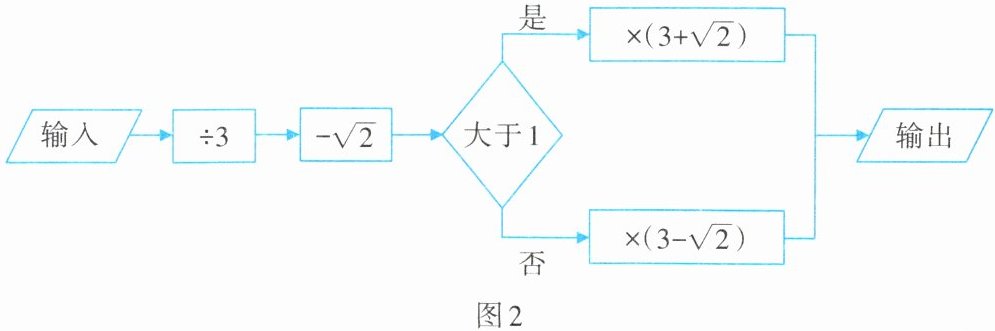
9. 按如图2所示的运算程序,若输入数字“9”,则输出的结果是( ).

A. $11-6\sqrt {2}$
B. 1
C. $11-3\sqrt {2}$
D. 7

答案： 【解析】：
当输入数字“$9$”时，
第一步：$9\div3 = 3$；
第二步：$3-\sqrt{2}$；
第三步：比较$3 - \sqrt{2}$与$1$的大小，因为$\sqrt{2}\approx1.414$，所以$3-\sqrt{2}\approx3 - 1.414=1.586\gt1$；
第四步：因为$3-\sqrt{2}\gt1$，所以$(3 - \sqrt{2})\times(3+\sqrt{2})$，根据平方差公式$(a + b)(a - b)=a^{2}-b^{2}$，这里$a = 3$，$b=\sqrt{2}$，则$(3 - \sqrt{2})\times(3+\sqrt{2})=3^{2}-(\sqrt{2})^{2}=9 - 2=7$。
【答案】：D