《2025年暑假乐园海南出版社八年级数学人教版》

4. 如图10，四边形$ABCD$是长方形，把$△ACD$沿$AC$折叠到$△ACD'$，$AD'$与$BC$交于点$E$，已知$AD = 4$，$DC = 3$。
(1)求$AC$的长度；
(2)求$BE$的长度。

答案： 【解析】：
(1)在长方形$ABCD$中，$\angle D = 90^{\circ}$，根据勾股定理$AC=\sqrt{AD^{2}+DC^{2}}$，已知$AD = 4$，$DC = 3$，则$AC=\sqrt{4^{2}+3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5$。
(2)因为四边形$ABCD$是长方形，所以$AD// BC$，$\angle B = 90^{\circ}$，$AB = DC = 3$，$BC = AD = 4$。
由折叠可知$\angle DAC=\angle D'AC$，又因为$AD// BC$，所以$\angle DAC=\angle ACB$，那么$\angle D'AC=\angle ACB$，所以$AE = EC$。
设$BE = x$，则$EC = 4 - x$，$AE = 4 - x$。
在$Rt\triangle ABE$中，根据勾股定理$AB^{2}+BE^{2}=AE^{2}$，即$3^{2}+x^{2}=(4 - x)^{2}$。
展开$(4 - x)^{2}=16-8x+x^{2}$，则$9+x^{2}=16-8x+x^{2}$，
移项可得$8x=16 - 9$，$8x = 7$，解得$x=\frac{7}{8}$。
【答案】：
(1)$5$；
(2)$\frac{7}{8}$。

综合与实践。
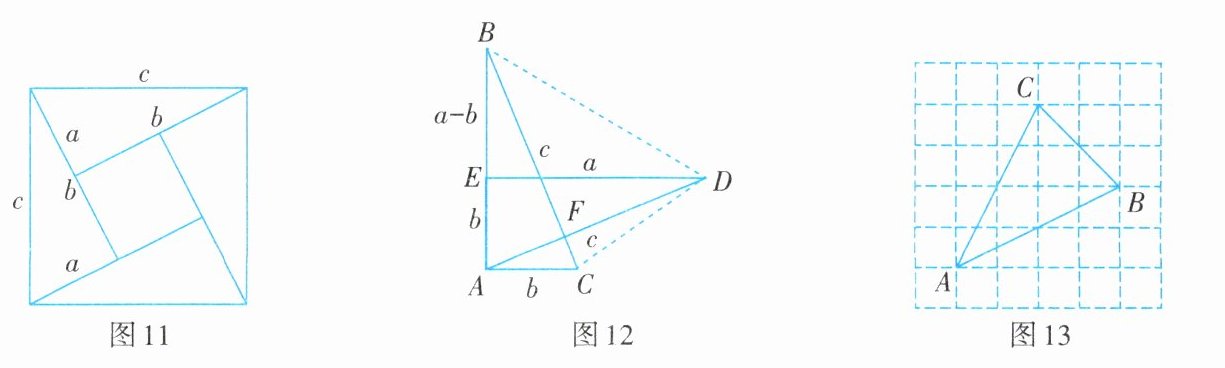
勾股定理是几何学中的明珠，充满着魅力。图11是著名的赵爽弦图，由四个全等的直角三角形拼成，用它可以证明勾股定理。图11的大正方形面积有两种求法，一种是等于大正方形的边长乘边长，即$c^{2}$；另一种是等于四个直角三角形与一个小正方形的面积之和，即$\frac{1}{2}ab×4+(b - a)^{2}$。因此，$c^{2}=\frac{1}{2}ab×4+(b - a)^{2}$，化简便得结论$a^{2}+b^{2}=c^{2}$。用两种不同的方式表示同一个量，从而建立等式或方程。这种方法在代数、几何等多个领域都有广泛应用，能够帮助我们将实际问题转化为数学方程，进而求解未知数。

(1)方法运用
千百年来，勾股定理的证明吸引着无数人投身其中，既有著名的数学家，也有数学业余爱好者。向常春在2010年发现了一个新的证法：把两个全等的$Rt△ABC$和$Rt△DEA$如图12放置，其三边长分别为$a$，$b$，$c$，$∠BAC = ∠DEA = 90^{\circ}$，显然$BC⊥AD$。
请用$a$，$b$，$c$分别表示出四边形$ABDC$，梯形$AEDC$，$△EBD$的面积，再探究这三个图形面积之间的关系，证明勾股定理$a^{2}+b^{2}=c^{2}$。
(2)方法迁移
如图13，小正方形边长为1，连接小正方形的三个顶点，可得$△ABC$，则$S_{△ABC}$为______，$AB$边上的高为______。

答案： 【解析】：
(1)首先求四边形$ABDC$的面积$S_{ABDC}$：因为四边形$ABDC$是由两个全等的直角三角形$Rt\triangle ABC$和$Rt\triangle DEA$组成，且$Rt\triangle ABC$的面积$S_{\triangle ABC}=\frac{1}{2}ab$，所以$S_{ABDC}=2\times\frac{1}{2}ab = ab$。然后求梯形$AEDC$的面积$S_{梯形AEDC}$：梯形的面积公式为$S=\frac{1}{2}(上底 + 下底)\times高$，在梯形$AEDC$中，上底$AE = a$，下底$CD = b$，高$ED + AC=a + b$，则$S_{梯形AEDC}=\frac{1}{2}(a + b)(a + b)=\frac{1}{2}(a^{2}+2ab + b^{2})$。接着求$\triangle EBD$的面积$S_{\triangle EBD}$：在$\triangle EBD$中，$EB=AB - AE=c - a$，$ED = a$，$BD=AD - AB=b - c$，根据勾股定理可知$S_{\triangle EBD}=\frac{1}{2}(c - a)(b - c)=\frac{1}{2}(bc - c^{2}-ab + ac)$。最后探究面积关系证明勾股定理：由$S_{梯形AEDC}=S_{ABDC}+S_{\triangle EBD}$可得：$\frac{1}{2}(a^{2}+2ab + b^{2})=ab+\frac{1}{2}(bc - c^{2}-ab + ac)$等式两边同时乘以$2$得：$a^{2}+2ab + b^{2}=2ab+bc - c^{2}-ab + ac$因为$S_{梯形AEDC}=S_{ABDC}+S_{\triangle EBD}$还可以从另一个角度看，$S_{梯形AEDC}=\frac{1}{2}(a + b)(a + b)$，$S_{ABDC}=2\times\frac{1}{2}ab$，$S_{\triangle EBD}=\frac{1}{2}c^{2}$所以$\frac{1}{2}(a + b)(a + b)=2\times\frac{1}{2}ab+\frac{1}{2}c^{2}$展开$\frac{1}{2}(a^{2}+2ab + b^{2})=ab+\frac{1}{2}c^{2}$等式两边同时乘以$2$得：$a^{2}+2ab + b^{2}=2ab + c^{2}$移项可得$a^{2}+b^{2}=c^{2}$。
(2)求$S_{\triangle ABC}$：用一个大正方形的面积减去三个直角三角形的面积来求$\triangle ABC$的面积。大正方形的边长为$3$，其面积$S = 3\times3=9$。三个直角三角形的面积分别为：$S_1=\frac{1}{2}\times2\times1 = 1$，$S_2=\frac{1}{2}\times2\times3 = 3$，$S_3=\frac{1}{2}\times1\times3=\frac{3}{2}$。则$S_{\triangle ABC}=9-(1 + 3+\frac{3}{2})=9 - \frac{2 + 6+3}{2}=9-\frac{11}{2}=\frac{7}{2}$。求$AB$边上的高$h$：先根据勾股定理求$AB$的长度，$AB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$。根据三角形面积公式$S=\frac{1}{2}\times底\times高$，已知$S_{\triangle ABC}=\frac{7}{2}$，底$AB = \sqrt{5}$，则$\frac{1}{2}\times\sqrt{5}\times h=\frac{7}{2}$，解得$h=\frac{7\sqrt{5}}{5}$。【答案】：
(2)$\frac{7}{2}$；$\frac{7\sqrt{5}}{5}$