2025年时习之暑假衔接八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 在平面直角坐标系中,二次函数$y = a ( x - 3 ) ^ { 2 }$($a \neq 0$)的图象可能是( )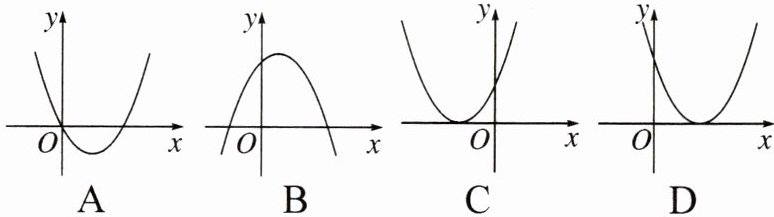

答案:
D
3. 抛物线$y = - 2 ( x - 3 ) ^ { 2 }$的开口____,对称轴是____,顶点坐标是____,当$x$____时,$y随x$的增大而增大,当$x$____时,$y随x$的增大而减小。
答案:
向下 直线$ x=3 $ $(3,0)$ $ <3 $ $ >3 $
4. 将抛物线$y = ( x + 1 ) ^ { 2 }$向右平移2个单位长度,得到新抛物线的顶点坐标是____。
答案:
$(1,0)$
5. 已知抛物线$y = ( x - 2 ) ^ { 2 }上有两点A ( 0 , y _ { 1 } )和B ( 3 , y _ { 2 } )$,则$y _ { 1 }$____$y _ { 2 }$(填“$>$”“$<$”或“$=$”)。
答案:
$ > $
6. 已知二次函数$y = - ( x - h ) ^ { 2 }$,当$x < - 2$时,$y随着x$的增大而增大;当$x > - 2$时,$y随x$的增大而减小,则$h$的值为____。
答案:
-2
7. 已知二次函数$y = a ( x - h ) ^ { 2 }图象的顶点坐标是( - 5 , 0 )$,且过点$( 0 , - 3 )$。
(1)求二次函数的解析式;
(2)当$x$为何值时,函数值$y$有最值?
(1)求二次函数的解析式;
(2)当$x$为何值时,函数值$y$有最值?
答案:
7.解:
(1)
∵二次函数$y=a(x-h)^2$图象的顶点坐标是$(-5,0)$,
∴$ h=-5 $,即二次函数的解析式为$ y=a(x+5)^2 $.
∵二次函数图象过点$(0,-3)$,
∴$ a(0+5)^2=-3 $,解得$ a=-\dfrac{3}{25} $.
∴二次函数的解析式为$ y=-\dfrac{3}{25}(x+5)^2 $.
(2)
∵对称轴为直线$ x=-5 $,
∴当$ x=-5 $时,函数值 y 有最值.
(1)
∵二次函数$y=a(x-h)^2$图象的顶点坐标是$(-5,0)$,
∴$ h=-5 $,即二次函数的解析式为$ y=a(x+5)^2 $.
∵二次函数图象过点$(0,-3)$,
∴$ a(0+5)^2=-3 $,解得$ a=-\dfrac{3}{25} $.
∴二次函数的解析式为$ y=-\dfrac{3}{25}(x+5)^2 $.
(2)
∵对称轴为直线$ x=-5 $,
∴当$ x=-5 $时,函数值 y 有最值.
8. 如图是二次函数$y = a ( x + m ) ^ { 2 }$的图象。
(1)求二次函数的解析式;
(2)把抛物线$y = a x ^ { 2 }$经过怎样的平移才能得到此抛物线?
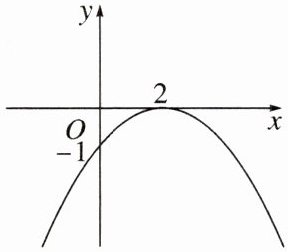
(1)求二次函数的解析式;
(2)把抛物线$y = a x ^ { 2 }$经过怎样的平移才能得到此抛物线?

答案:
8.解:
(1)由图象可知,顶点坐标为$(2,0)$,
∴$ m=-2 $).
∴二次函数的解析式为$ y=a(x-2)^2 $.将$(0,-1)$代入得$-1=4a$,解得$ a=-\dfrac{1}{4} $.
∴二次函数的解析式为$ y=-\dfrac{1}{4}(x-2)^2 $.
(2)由
(1)得$ a=-\dfrac{1}{4} $,将抛物线$ y=-\dfrac{1}{4}x^2 $向右平移2 个单位长度即可得到抛物线$ y=-\dfrac{1}{4}(x-2)^2 $.
(1)由图象可知,顶点坐标为$(2,0)$,
∴$ m=-2 $).
∴二次函数的解析式为$ y=a(x-2)^2 $.将$(0,-1)$代入得$-1=4a$,解得$ a=-\dfrac{1}{4} $.
∴二次函数的解析式为$ y=-\dfrac{1}{4}(x-2)^2 $.
(2)由
(1)得$ a=-\dfrac{1}{4} $,将抛物线$ y=-\dfrac{1}{4}x^2 $向右平移2 个单位长度即可得到抛物线$ y=-\dfrac{1}{4}(x-2)^2 $.
9. 如图,抛物线$y = ( x - h ) ^ { 2 }与x轴只有一个交点M$,且与平行于$x轴的直线l交于A$,$B$两点,若$AB = 3$,求点$M到直线l$的距离。
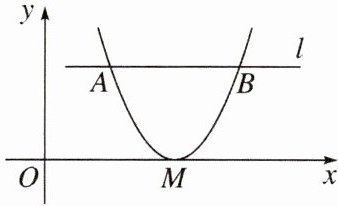

答案:
9.解:由题意得抛物线的顶点坐标为$ M(h,0) $,设点 M到直线 l 的距离为 a,则$(x-h)^2=a$,解得$ x=h\pm\sqrt{a} $,即$ A(h-\sqrt{a},a) $,$ B(h+\sqrt{a},a) $.
∵$ AB=3 $,
∴$ h+\sqrt{a}-(h-\sqrt{a})=3 $,解得$ a=\dfrac{9}{4} $.
∵$ AB=3 $,
∴$ h+\sqrt{a}-(h-\sqrt{a})=3 $,解得$ a=\dfrac{9}{4} $.
查看更多完整答案,请扫码查看


