2025年时习之暑假衔接八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 某航空公司规定,旅客乘机携带行李的质量x(千克)与其运费y(元)的关系由如图所示的一次函数图象确定,则旅客可免费携带行李的最大质量为 ( )

A.20千克
B.25千克
C.28千克
D.30千克

A.20千克
B.25千克
C.28千克
D.30千克
答案:
A
2. 小红爸爸的公司急需用车,但又不准备买车,公司准备和一个个体车主或一家出租车公司签订月租车合同,设汽车每月行驶x千米,个体车主收费为$y_1$元,出租车公司收费为$y_2$元,观察图象可知,当x______时,选用个体车主较合算.
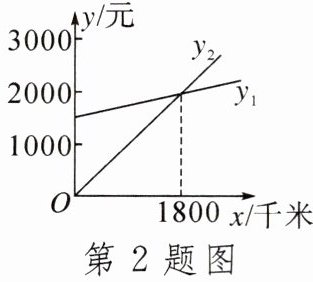

答案:
>1800
3. 甲、乙两人进行赛跑,甲比乙跑得快,现在甲让乙先跑10米,甲再起跑. 图中$l_1$和$l_2$分别表示甲、乙两人跑步的路程y(m)与甲跑步的时间x(s)之间的函数关系,其中$l_1$的解析式为$y_1= 8x,$问甲追上乙用了多长时间?
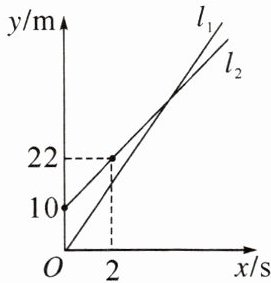

答案:
解:设y₂=kx+b(k≠0),根据题意,可得方程组
{10=b,
22=2k+b,
解得{k=6,
b=10.
∴y₂=6x+10.当y₁=y₂时,8x=6x+10,解得x=5.
答:甲追上乙用了5s.
{10=b,
22=2k+b,
解得{k=6,
b=10.
∴y₂=6x+10.当y₁=y₂时,8x=6x+10,解得x=5.
答:甲追上乙用了5s.
4. 某商店销售甲、乙两种商品. 下表为两次销售记录:
| | 甲商品/个 | 乙商品/个 | 总销售额/元 |
| 第一次 | 50 | 40 | 500 |
| 第二次 | 60 | 30 | 420 |
(1) 求甲和乙的销售单价分别是多少.
(2) 该商场计划再次购进两种商品共100个,根据市场实际需求,甲的数量不低于乙数量的4倍. 已知甲的进价为1元/个,乙的进价为6元/个. 设购买甲x个,获得的利润为W元.
① 求W关于x的函数关系式,并求出自变量x的取值范围.
② 该商店应如何进货才能使销售总利润最大? 并求出最大利润.
| | 甲商品/个 | 乙商品/个 | 总销售额/元 |
| 第一次 | 50 | 40 | 500 |
| 第二次 | 60 | 30 | 420 |
(1) 求甲和乙的销售单价分别是多少.
(2) 该商场计划再次购进两种商品共100个,根据市场实际需求,甲的数量不低于乙数量的4倍. 已知甲的进价为1元/个,乙的进价为6元/个. 设购买甲x个,获得的利润为W元.
① 求W关于x的函数关系式,并求出自变量x的取值范围.
② 该商店应如何进货才能使销售总利润最大? 并求出最大利润.
答案:
(1)设甲的销售单价为a元/个,乙的销售单价为b元/个.由题意,得{50a+40b=500,
60a+30b=420,
解得{a=2,
b=10.
答:甲和乙的销售单价分别是2元/个、10元/个.
(2)①由题意,得W=(2-1)x+(10-6)×(100-x)=-3x+400,
∵甲的数量不低于乙数量的4倍,
∴x≥4×(100-x),解得x≥80.
∴W=-3x+400(80≤x≤100).
②对于W=-3x+400(80≤x≤100),
∵-3<0,
∴W随x的增大而减小.
∴当x=80时,W取得最大值,此时W=160,100-x=20.
答:该商店购进甲80个,乙20个才能使销售总利润最大,最大利润是160元.
(1)设甲的销售单价为a元/个,乙的销售单价为b元/个.由题意,得{50a+40b=500,
60a+30b=420,
解得{a=2,
b=10.
答:甲和乙的销售单价分别是2元/个、10元/个.
(2)①由题意,得W=(2-1)x+(10-6)×(100-x)=-3x+400,
∵甲的数量不低于乙数量的4倍,
∴x≥4×(100-x),解得x≥80.
∴W=-3x+400(80≤x≤100).
②对于W=-3x+400(80≤x≤100),
∵-3<0,
∴W随x的增大而减小.
∴当x=80时,W取得最大值,此时W=160,100-x=20.
答:该商店购进甲80个,乙20个才能使销售总利润最大,最大利润是160元.
查看更多完整答案,请扫码查看


