《2025年时习之暑假衔接八年级数学人教版》

9. 在平面直角坐标系中,一次函数 $ y = 2 x + 3 $ 的图象是( )

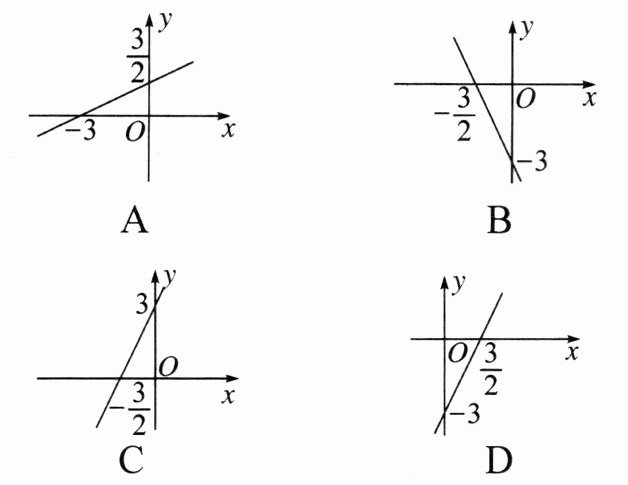
答案： C

10. 一次函数 $ y = - 2 x + 5 $ 的图象不经过( )

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： C

11. 将一次函数 $ y = 3 x - 1 $ 的图象沿 $ y $ 轴向上平移 3 个单位长度后,得到的图象对应的函数解析式为______.

答案： y=3x+2

12. 已知在一次函数 $ y = - 1.5 x + 3 $ 的图象上,有三点 $ ( - 3 , y _ { 1 } ) , ( - 1 , y _ { 2 } ) , ( 2 , y _ { 3 } ) $,则 $ y _ { 1 } , y _ { 2 } , y _ { 3 } $ 的大小关系为( )

A.$ y _ { 1 } ＞ y _ { 2 } ＞ y _ { 3 } $
B.$ y _ { 1 } ＞ y _ { 3 } ＞ y _ { 2 } $
C.$ y _ { 2 } ＞ y _ { 1 } ＞ y _ { 3 } $
D.无法确定

答案： A

13. 一次函数 $ y = ( m + 2 ) x + 1 $,若 $ y $ 随 $ x $ 的增大而增大,则 $ m $ 的取值范围是______.

答案： m＞-2

14. 请你任意写出一个经过点 $ ( 0 , 3 ) $,且 $ y $ 随 $ x $ 的增大而减小的一次函数的解析式：______.

答案： y=-x+3(答案不唯一)

15. 已知一次函数 $ y = ( 2 m + 4 ) x + ( 3 - m ) $.
(1)若图象经过第一、二、三象限,求 $ m $ 的取值范围；
(2)若 $ m = 1 $,当 $ - 1 \leq x \leq 2 $ 时,求 $ y $ 的取值范围.

答案： 解:
(1)根据题意得{2m+4＞0,3-m＞0,解得-2＜m＜3.
(2)将m=1代入y=(2m+4)x+(3-m),得y=6x+2.当x=-1时,y=-4;当x=2时,y=14.
∵k=6＞0,
∴y随x的增大而增大.
∴当-1≤x≤2时,-4≤y≤14.

16. 点 $ ( 3 , - 5 ) $ 在正比例函数 $ y = k x ( k \neq 0 ) $ 的图象上,则 $ k $ 的值为( )

A.-15
B.15
C.$ - \frac { 3 } { 5 } $
D.$ - \frac { 5 } { 3 } $

答案： D

17. 已知一次函数 $ y = a x + b $($ a $,$ b $ 为常数,且 $ a \neq 0 $)的图象经过点 $ ( 1 , 3 ) $ 和 $ ( 0 , - 2 ) $,则 $ a - b $ 的值为( )

A.-1
B.-3
C.3
D.7

答案： D

18. 如果直线 $ y = - 2 x + 1 $ 平移后经过点 $ A ( 2 , 3 ) $,那么平移后的直线解析式是______.

答案： y=-2x+7

19. 已知 $ y $ 是关于 $ x $ 的一次函数. 如果当 $ y = 1 $ 时,$ x = - 2 $；当 $ x = 3 $ 时,$ y = 6 $. 求 $ y $ 关于 $ x $ 的函数解析式.

答案： 解:设y关于x的函数解析式为y=kx+b.依题意得{-2k+b=1,3k+b=6,解得{k=1,b=3.
∴y关于x的函数解析式为y=x+3.

20. 已知一次函数的图象过 $ M ( 1 , 3 ) $,$ N ( - 2 , 12 ) $ 两点.
(1)求一次函数的解析式；
(2)试判断点 $ P ( 2 a , - 6 a + 8 ) $ 是否在该函数的图象上,并说明理由.

答案： 解:
(1)设一次函数的解析式为y=kx+b,由题意,得{3=k+b,12=-2k+b解得{k=-3,b=6.
∴y=-3x+6.
(2)当x=2a时,y=-3×2a+6=-6a+6≠-6a+8,
∴点P(2a,-6a+8)不在该函数的图象上.