《2025年时习之暑假衔接八年级数学人教版》

例1 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为$20m^2$的矩形空地,求原正方形空地的边长。

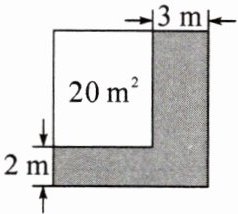
导析：可设原正方形的边长为x m,则剩余空地的长为(x - 2)m,宽为(x - 3)m。根据长方形的面积公式列方程求解即可。
解答：设原正方形空地的边长为x m,则剩余矩形空地的两边长分别为(x - 2)m与(x - 3)m。
根据题意,得(x - 3)(x - 2) = 20,解得$x_1 = 7,x_2 = -2($不合题意,舍去)。
答：原正方形空地的边长为7m。

答案： 【解析】：本题主要考查一元二次方程的应用。
设原正方形的边长为$x$m，
那么，当一边减少了$2$m，另一边减少了$3$m，
剩余矩形的长为$(x - 2)$m，宽为$(x - 3)$m。
根据矩形的面积公式：$面积 = 长 × 宽$。
由题可知，剩余矩形的面积是$20m^2$，
所以可以列出方程：
$(x - 3)(x - 2) = 20$。
展开并整理这个方程，得到：
$x^2 - 5x + 6 = 20$。
$x^2 - 5x - 14 = 0$。
通过因式分解或者使用求根公式，可以得到方程的解为：
$x_1 = 7$，$x_2 = -2$。
由于边长不能为负数，
所以舍去$x_2 = -2$这个解。
【答案】：原正方形空地的边长为$7$m。

1. 如图,某小区要在长为16m,宽为12m的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为______m。

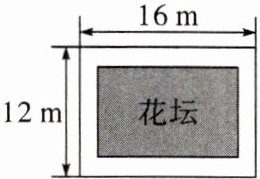
答案： 2

例2 如图,某校生物小组有一块长为32m,宽为20m的矩形试验田,为了方便管理,准备纵、横各开辟一条等宽的小道(图中阴影部分)。要使种植面积为$540m^2,$小道的宽应是多少？

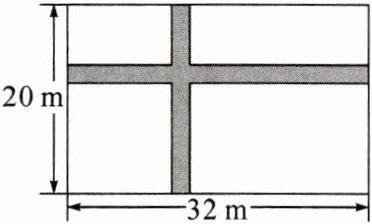
导析：本题可设道路的宽为x m,将4块草地平移为一个长方形,长为(32 - x)m,宽为(20 - x)m。根据长方形面积公式即可求出道路的宽。
解答：设道路的宽为x m,依题意有(32 - x)(20 - x) = 540,整理,得$x^2 - 52x + 100 = 0。$∴(x - 50)(x - 2) = 0。∴$x_1 = 2,x_2 = 50($不合题意,舍去)。
答：小道的宽应是2m。
方法归纳：解决“小路”问题时,可以利用平移将问题转化为类“边框”问题,再进行解答。

答案： 【解析】：
本题考查了一元二次方程的应用，利用平移将不规则图形变为规则图形是解题的关键。
设小道的宽为$x$m，则种植部分的长为$(32 - x)$m，宽为$(20 - x)$m。
根据矩形的面积公式：面积 = 长 × 宽，我们可以得到种植部分的面积为：
$(32 - x)(20 - x)$
依题意，这个面积应该等于$540m^2$，所以我们有方程：
$(32 - x)(20 - x) = 540$
展开并整理得：
$x^2 - 52x + 100 = 0$
因式分解该方程：
$(x - 2)(x - 50) = 0$
解得：
$x_1 = 2, x_2 = 50$
由于小道的宽度不可能超过矩形试验田的宽度（20m），所以$x_2 = 50$不合题意，应舍去。
【答案】：
小道的宽应是$2$m。

2. 如图,某小区计划在一个长为24m,宽为10m的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草。若草坪部分的总面积为$126m^2,$则小路的宽度为______m。

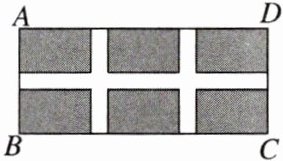
答案： 3

例3 如图,现有总长为12m的建筑材料,借助一面6m长的砖墙MN,围成一个矩形场地ABCD。已知长方形场地的面积为$16m^2,$求AB的长。

导析：设AB的长为x m,然后表示出BC的长为(12 - 2x)m,利用矩形的面积计算方法列出方程求解即可。
解答：设AB为x m,则BC为(12 - 2x)m。由题意,得x(12 - 2x) = 16,解得$x_1 = 4,x_2 = 2。$当x = 4时,12 - 2x = 4 ＜ 6；当x = 2时,12 - 2x = 8 ＞ 6(不合题意,舍去)。
答：AB的长为4m。
方法归纳：解决“围墙”问题时,要注意题目中是否给出墙的长,求出结果后,需要判断与墙平行的一边的长是否超出墙的长,根据实际情况进行取舍。

答案： 【解析】：
本题是一个典型的面积问题，需要利用矩形的面积公式进行求解。
设AB的长为$x$米，由于总长是12米，且一面是砖墙，所以$BC$的长就是$(12 - 2x)$米（两个AB和两个BC的总长是12米，其中一个BC是靠墙的，所以不计入总长的$x$倍中）。
根据矩形的面积公式：$\text{面积} = \text{长} × \text{宽}$，可以列出方程：
$x(12 - 2x) = 16$，
解这个方程，得到两个解，$x_1 = 4$ 和 $x_2 = 2$。
当 $x = 4$ 时，$BC = 12 - 2 × 4 = 4$ 米，小于墙的长度6米，符合题意。
当 $x = 2$ 时，$BC = 12 - 2 × 2 = 8$ 米，大于墙的长度6米，不符合题意，所以舍去。
【答案】：
解：设AB为$x$m，则BC为$(12 - 2x)$m。
由题意，得：
$x(12 - 2x) = 16$，
解得：$x_1 = 4$，$x_2 = 2$。
当$x = 4$时，$12 - 2x = 4 \lt 6$；
当$x = 2$时，$12 - 2x = 8 \gt 6$（不合题意,舍去）。
答：AB的长为4m。