2025年时习之暑假衔接八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在矩形ABCD中,对角线AC,BD交于点O。若∠AOB= 50°,则∠ADB的度数为( )
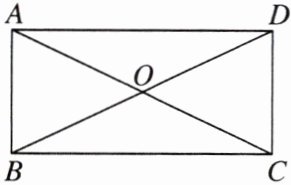
A.65°
B.50°
C.25°
D.20°

A.65°
B.50°
C.25°
D.20°
答案:
C
2. 如图,要使□ABCD成为矩形,需要添加的条件是( )
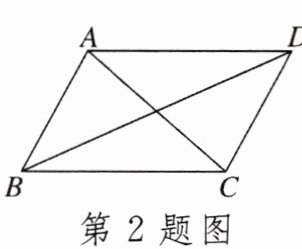
A.∠ABD= ∠CBD
B.AC= BD
C.AC⊥BD
D.AB= BC

A.∠ABD= ∠CBD
B.AC= BD
C.AC⊥BD
D.AB= BC
答案:
B
3. 如图,在矩形ABCD中,点E在边BC上,点F是AE的中点,AB= 8,AD= DE= 10,则BF的长为______。
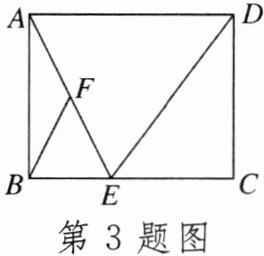

答案:
$2\sqrt{5}$
4. 在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,且DF= BE,连接AF,BF。
(1)求证:四边形BFDE是矩形;
(2)若CF= 3,BF= 4,AF平分∠DAB,求DF的长。
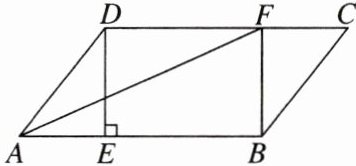
(1)求证:四边形BFDE是矩形;
(2)若CF= 3,BF= 4,AF平分∠DAB,求DF的长。

答案:
(1)证明:
∵ 四边形 ABCD 是平行四边形,
∴CD//AB.
∴DF//BE.又
∵DF=BE,
∴四边形 BFDE 是平行四边形.
∵DE⊥AB 于点 E,
∴∠BED=90°.
∴四边形 BFDE 是矩形.(2)解:易得∠BFD=90°,
∴∠BFC=90°.
∴BC=$\sqrt{CF^{2}+BF^{2}}=\sqrt{3^{2}+4^{2}}=5$.
∴AD=BC=5.
∵AF 平分∠DAB,
∴∠DAF=∠BAF.
∵CD//AB,
∴∠DFA=∠BAF.
∴∠DAF=∠DFA.
∴DF=AD=5.
∴DF 的长为 5.
∵ 四边形 ABCD 是平行四边形,
∴CD//AB.
∴DF//BE.又
∵DF=BE,
∴四边形 BFDE 是平行四边形.
∵DE⊥AB 于点 E,
∴∠BED=90°.
∴四边形 BFDE 是矩形.(2)解:易得∠BFD=90°,
∴∠BFC=90°.
∴BC=$\sqrt{CF^{2}+BF^{2}}=\sqrt{3^{2}+4^{2}}=5$.
∴AD=BC=5.
∵AF 平分∠DAB,
∴∠DAF=∠BAF.
∵CD//AB,
∴∠DFA=∠BAF.
∴∠DAF=∠DFA.
∴DF=AD=5.
∴DF 的长为 5.
查看更多完整答案,请扫码查看


