《2025年时习之暑假衔接八年级数学人教版》

3. 已知两个连续正偶数的积为224,则这两个连续正偶数的和是______。

答案： 30

1. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是73。设每个支干长出x个小分支,则可列方程为( )
$A. 1+x+x^2= 73$
$B. (1+x)^2= 73$
$C. x+x^2= 73$
$D. 1+(1+x)+(1+x)^2= 73$

答案： A

2. 在某商品交易会上每两家公司之间都签订了一份合同,所有公司共签订了45份合同。设共有x家公司参加商品交易会,则x满足的方程为$( )A. \frac{1}{2}x(x+1)= 45B. \frac{1}{2}x(x-1)= 45C. x(x+1)= 45D. x(x-1)= 45$

答案： B

3. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,应邀请多少个队参加比赛？设应邀请x个队参加比赛,则x的值为( )

A.7
B.8
C.9
D.10

答案： A

4. 某班同学毕业时每人都将自己的照片向其他同学各送一张表示留念,全班共送1056张照片。设全班有x名同学,则根据题意,可列方程为______。

答案： $x(x-1)=1056$

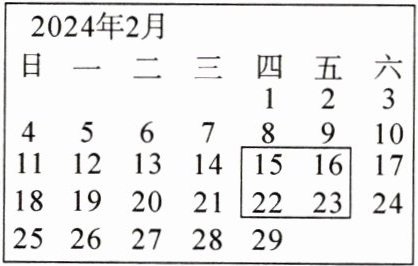
5. 在2024年2月的月历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,则这个最小数为______。

答案： 5

6. 化学课代表在老师的培训下,学会了用高锰酸钾制取氧气的实验室制法,回到班上后,第一节课手把手教会了若干名同学,第二节课会做该实验的每个同学又手把手教会了同样多的同学,这样全班49人恰好都会做这个实验了。问一个人每节课手把手教会了多少名同学？

答案： 解:设一个人每节课手把手教会了x名同学,根据题意,得$(1+x)^{2}=49$,解得$x_{1}=6$,$x_{2}=-8$(不符合题意,舍去).答:一个人每节课手把手教会了6名同学.

7. 第十四届国际数学教育大会(ICME-14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745。八进制是以8作为进位基数的数字系统,有0~7共8个基本数字,八进制数3745换算成十进制数是$3×8^3+7×8^2+4×8^1+5×8⁰= 2021,$表示ICME-14的举办年份。
(1)请把八进制数3747换算成十进制数；
(2)小华设计了一个n进制数265,换算成十进制数是145,求n的值(n为正整数)。

答案：
(1)$3×8^{3}+7×8^{2}+4×8^{1}+7×8^{0}=1536+448+32+7=2023$.
(2)依题意有$2n^{2}+6n+5=145$,解得$n_{1}=7$,$n_{2}=-10$(舍去).故n的值是7.