2025年时习之暑假衔接八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
例1 在平面直角坐标系内,画出二次函数$y = x^{2}+1$的图象,并根据图象回答下列问题:
(1)函数$y = x^{2}+1$,当$x$____时,$y随x$的增大而减小;当$x$____时,函数$y$有最小值,最小值是____;其图象与$y$轴交点的坐标是____。
(2)试写出抛物线$y = -x^{2}-1$的开口方向、对称轴和顶点坐标。
解答:列表:
| $x$ | …$$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $y = x^{2}+1$ | …$$ | $5$ | $2$ | $1$ | $2$ | $5$ | …$$ |
函数$y = x^{2}+1$的图象如图所示:
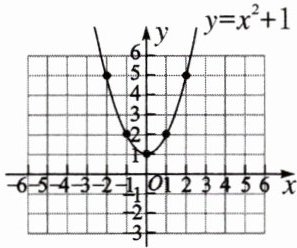
(1)$<0$ $=0$ $1$ $(0,1)$
(2)抛物线$y = -x^{2}-1$的开口向下,对称轴是$y$轴,顶点坐标是$(0,-1)$
(1)函数$y = x^{2}+1$,当$x$____时,$y随x$的增大而减小;当$x$____时,函数$y$有最小值,最小值是____;其图象与$y$轴交点的坐标是____。
(2)试写出抛物线$y = -x^{2}-1$的开口方向、对称轴和顶点坐标。
解答:列表:
| $x$ | …$$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $y = x^{2}+1$ | …$$ | $5$ | $2$ | $1$ | $2$ | $5$ | …$$ |
函数$y = x^{2}+1$的图象如图所示:

(1)$<0$ $=0$ $1$ $(0,1)$
(2)抛物线$y = -x^{2}-1$的开口向下,对称轴是$y$轴,顶点坐标是$(0,-1)$
答案:
【解析】:
本题主要考查二次函数$y = ax^{2}+k$的图象和性质。
首先,我们可以通过列表、描点、连线的方法画出二次函数$y = x^{2}+1$的图象。
然后,根据图象,我们可以回答以下问题:
(1)对于函数$y = x^{2}+1$,因为$a=1\gt0$,
所以其图象是一个开口向上的抛物线,对称轴为$y$轴,顶点为$(0,1)$。
因此,当$x \lt 0$时,$y$随$x$的增大而减小;
当$x = 0$时,函数$y$有最小值,最小值是$1$;
其图象与$y$轴交点的坐标是$(0,1)$。
(2)对于抛物线$y = -x^{2}-1$,因为$a=-1\lt0$,
所以其图象是一个开口向下的抛物线,对称轴为$y$轴,顶点为$(0,-1)$。
【答案】:
(1)$<0$;$=0$;$1$;$(0,1)$
(2)抛物线$y = -x^{2}-1$的开口向下,对称轴是$y$轴,顶点坐标是$(0,-1)$
本题主要考查二次函数$y = ax^{2}+k$的图象和性质。
首先,我们可以通过列表、描点、连线的方法画出二次函数$y = x^{2}+1$的图象。
然后,根据图象,我们可以回答以下问题:
(1)对于函数$y = x^{2}+1$,因为$a=1\gt0$,
所以其图象是一个开口向上的抛物线,对称轴为$y$轴,顶点为$(0,1)$。
因此,当$x \lt 0$时,$y$随$x$的增大而减小;
当$x = 0$时,函数$y$有最小值,最小值是$1$;
其图象与$y$轴交点的坐标是$(0,1)$。
(2)对于抛物线$y = -x^{2}-1$,因为$a=-1\lt0$,
所以其图象是一个开口向下的抛物线,对称轴为$y$轴,顶点为$(0,-1)$。
【答案】:
(1)$<0$;$=0$;$1$;$(0,1)$
(2)抛物线$y = -x^{2}-1$的开口向下,对称轴是$y$轴,顶点坐标是$(0,-1)$
1. 关于二次函数$y = -2x^{2}+3$的下列结论,正确的是( )
A.它的开口方向是向上
B.当$x<-1$时,$y随x$的增大而增大
C.它的顶点坐标是$(-2,3)$
D.当$x = 0$时,$y取最小值3$
A.它的开口方向是向上
B.当$x<-1$时,$y随x$的增大而增大
C.它的顶点坐标是$(-2,3)$
D.当$x = 0$时,$y取最小值3$
答案:
B
例2 把二次函数$y = -3x^{2}的图象向上平移5$个单位长度后所得的图象的函数解析式是( )
A.$y = -3(x - 5)^{2}$
B.$y = -3(x + 5)^{2}$
C.$y = -3x^{2}+5$
D.$y = -3x^{2}-5$
导析:根据“上加下减”的法则解答即可。
解答:C
A.$y = -3(x - 5)^{2}$
B.$y = -3(x + 5)^{2}$
C.$y = -3x^{2}+5$
D.$y = -3x^{2}-5$
导析:根据“上加下减”的法则解答即可。
解答:C
答案:
【解析】:
本题考查的是二次函数图象的平移性质。对于函数$y = ax^{2} + k$,当图象向上平移b个单位时,新的函数解析式变为$y = ax^{2} + k + b$;当图象向下平移b个单位时,新的函数解析式变为$y = ax^{2} + k - b$。这是基于“上加下减”的法则,即在上加,向下减。
对于给定的函数$y = -3x^{2}$,其图象向上平移5个单位后,新的函数解析式应为$y = -3x^{2} + 5$。
【答案】:
C
本题考查的是二次函数图象的平移性质。对于函数$y = ax^{2} + k$,当图象向上平移b个单位时,新的函数解析式变为$y = ax^{2} + k + b$;当图象向下平移b个单位时,新的函数解析式变为$y = ax^{2} + k - b$。这是基于“上加下减”的法则,即在上加,向下减。
对于给定的函数$y = -3x^{2}$,其图象向上平移5个单位后,新的函数解析式应为$y = -3x^{2} + 5$。
【答案】:
C
2. 将抛物线$y = 2x^{2}平移后得到抛物线y = 2x^{2}+1$,则平移方式为( )
A.向左平移$1$个单位长度
B.向右平移$1$个单位长度
C.向上平移$1$个单位长度
D.向下平移$1$个单位长度
A.向左平移$1$个单位长度
B.向右平移$1$个单位长度
C.向上平移$1$个单位长度
D.向下平移$1$个单位长度
答案:
C
查看更多完整答案,请扫码查看


