2025年时习之暑假衔接八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
例2 如图,在△ABC中,D是BC上的一点,AB= AD,E,F分别是AC,BD的中点,EF= 3,则AC的长是( )
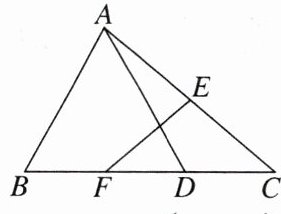
A.3 B.4 C.5 D.6
导析:连接AF.由AB= AD,F是BD的中点,根据等腰三角形三线合一的性质得出AF⊥BD.再根据直角三角形斜边上的中线等于斜边的一半求得EF= 1/2 AC,即AC= 2EF= 6.
解答:D

A.3 B.4 C.5 D.6
导析:连接AF.由AB= AD,F是BD的中点,根据等腰三角形三线合一的性质得出AF⊥BD.再根据直角三角形斜边上的中线等于斜边的一半求得EF= 1/2 AC,即AC= 2EF= 6.
解答:D
答案:
D
8.如图,在Rt△ABC中,AB= 4,点M是斜边BC的中点,以AM为边作正方形AMEF.若$S_{正方形AMEF}= 16,则S_{△ABC}= ( )A.4√3 B.8√3 C.12 D.16$
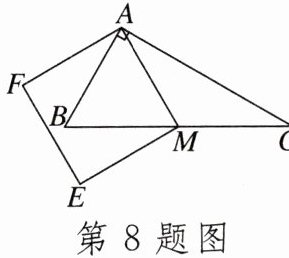

答案:
B
9.如图,在△ABC中,∠C= 25°,D在BC上,且DA⊥AC,AB= 1/2 DC,则∠BAC= ____°.


答案:
105
10.如图,在Rt△ABC中,∠ACB= 90°,点D、点F和点E分别是边AB,AD和AC的中点.若EF= 2,求AB的长.
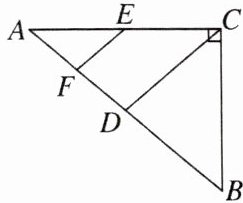

答案:
解:
∵E是AC的中点,F是AD的中点,
∴EF是△ACD的中位线.
∴CD=2EF=4.在Rt△ABC中,
∵D是AB的中点,
∴AB=2CD=8.
∵E是AC的中点,F是AD的中点,
∴EF是△ACD的中位线.
∴CD=2EF=4.在Rt△ABC中,
∵D是AB的中点,
∴AB=2CD=8.
11.如图,在Rt△ABC中,∠ACB= 90°,点D,E分别是AB,BC的中点,点F在AC的延长线上,∠FEC= ∠B.
(1)求证:DE= CF;
(2)若AC= 6 cm,AB= 10 cm,求四边形DCFE的面积.
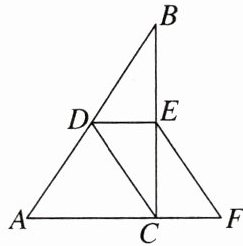
(1)求证:DE= CF;
(2)若AC= 6 cm,AB= 10 cm,求四边形DCFE的面积.

答案:
(1)证明:在△CDE和△ECF中,
∵∠ACB=∠ECF=90°,点D,E分别是AB,BC的中点,
∴CD=BD=AD,DE//AF.
∴∠B=∠DCE,∠CED=∠ECF=90°.又
∵∠FEC=∠B,
∴∠FEC=∠DCE.
∴EF//DC.又
∵DE//CF,
∴四边形DCFE是平行四边形.
∴DE=CF.
(2)解:在Rt△ABC中,
∵∠ACB=90°,
∴BC=$\sqrt{AB^2-AC^2}$=$\sqrt{10^2-6^2}$=8(cm).
∵点D,E分别是AB,BC的中点,
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3(cm),CE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4(cm).由
(1)知四边形DCFE是平行四边形,
∴S四边形DCFE=DE·CE=3×4=12(cm²).
(1)证明:在△CDE和△ECF中,
∵∠ACB=∠ECF=90°,点D,E分别是AB,BC的中点,
∴CD=BD=AD,DE//AF.
∴∠B=∠DCE,∠CED=∠ECF=90°.又
∵∠FEC=∠B,
∴∠FEC=∠DCE.
∴EF//DC.又
∵DE//CF,
∴四边形DCFE是平行四边形.
∴DE=CF.
(2)解:在Rt△ABC中,
∵∠ACB=90°,
∴BC=$\sqrt{AB^2-AC^2}$=$\sqrt{10^2-6^2}$=8(cm).
∵点D,E分别是AB,BC的中点,
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3(cm),CE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4(cm).由
(1)知四边形DCFE是平行四边形,
∴S四边形DCFE=DE·CE=3×4=12(cm²).
12.如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,连接DE,M,N分别是BC,DE的中点,连接MN.
(1)求证:MN⊥DE;
(2)若BC= 20,DE= 12,求△MDE的面积.
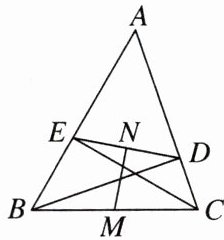
(1)求证:MN⊥DE;
(2)若BC= 20,DE= 12,求△MDE的面积.

答案:
(1)证明:连接ME,MD.
∵BD⊥AC,
∴∠BDC=90°.
∵M是BC的中点,
∴DM=$\frac{1}{2}$BC.同理可得EM=$\frac{1}{2}$BC,
∴DM=EM.
∵N是DE的中点,
∴MN⊥DE.
(2)解:
∵BC=20,ED=12,
∴DM=$\frac{1}{2}$BC=10,DN=$\frac{1}{2}$DE=6.由
(1)可知∠MND=90°,
∴MN=$\sqrt{MD^2-ND^2}$=$\sqrt{10^2-6^2}$=8.
∴S△MDE=$\frac{1}{2}$DE·MN=$\frac{1}{2}$×12×8=48.
(1)证明:连接ME,MD.
∵BD⊥AC,
∴∠BDC=90°.
∵M是BC的中点,
∴DM=$\frac{1}{2}$BC.同理可得EM=$\frac{1}{2}$BC,
∴DM=EM.
∵N是DE的中点,
∴MN⊥DE.
(2)解:
∵BC=20,ED=12,
∴DM=$\frac{1}{2}$BC=10,DN=$\frac{1}{2}$DE=6.由
(1)可知∠MND=90°,
∴MN=$\sqrt{MD^2-ND^2}$=$\sqrt{10^2-6^2}$=8.
∴S△MDE=$\frac{1}{2}$DE·MN=$\frac{1}{2}$×12×8=48.
查看更多完整答案,请扫码查看


