《2025年时习之暑假衔接八年级数学人教版》

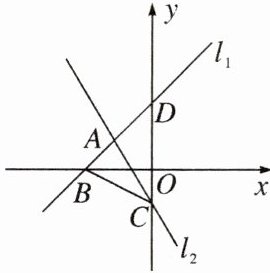
4.已知直线$l_{1}:y_{1}= x+2与直线l_{2}:y_{2}= kx-1$交于点A,点A的纵坐标为1,且直线$l_{1}$与x轴交于点B,与y轴交于点D,直线$l_{2}$与y轴交于点C.
(1)求直线$l_{2}$的解析式;
(2)连接BC,求$S_{△ABC}$.

答案： 4.解:
(1)当y=1时,x+2=1,解得x=-1,故点A的坐标为(-1,1).
∵点A在y₂=kx-1上,
∴-k-1=1,解得k=-2.
∴直线l₂的解析式为y₂=-2x-1.
(2)
∵直线l₁与x轴交于点B,
∴x+2=0,解得x=-2,即OB=2.
∵直线l₂与y轴交于点C,
∴点C的坐标为(0,-1),即OC=1.
∵直线l₁与y轴交于点D,
∴点D的坐标为(0,2),即OD=2.
∴DC=2+1=3.
∴S△ABC=1/2×3×2-1/2×3×1=3/2.

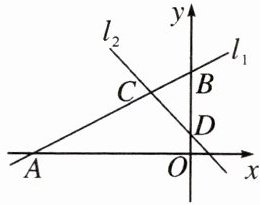
5.如图,在平面直角坐标系中,直线$l_{1}:y= kx+b$与x轴、y轴分别交于点$A(-8,0)$、点B,与直线$l_{2}:y= -x+1交于点C(m,3)$,直线$l_{2}$交y轴于点D.
(1)求m的值及直线$l_{1}$的解析式;
(2)求四边形AODC的面积.

答案： 5.解:
(1)点C(m,3)在直线l₂上,
∴-m+1=3,解得m=-2.
∴C(-2,3).把点A(-8,0),C(-2,3)代入直线l₁:y=kx+b中,得{-8k+b=0,-2k+b=3,解得{k=1/2,b=4.
∴直线l₁的解析式为y=1/2x+4.
(2)过点C作CE⊥x轴于点E,
∵A(-8,0),C(-2,3),
∴OA=8,OE=2,CE=3.
∴AE=8-2=6.
∵直线l₂:y=-x+1交y轴于点D,
∴D(0,1),故OD=1.
∴S四边形AODC=S△ACE+S梯形ODCE=1/2AE·CE+(OD+CE)·OE/2=1/2×6×3+(1+3)×2/2=13.故四边形AODC的面积为13.

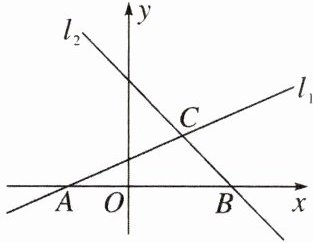
6.如图,直线$l_{1}$与x轴交于点$A(-2,0)$,与直线$l_{2}交于点C(m,m)$,直线$l_{2}$与x轴交于点B,已知直线$l_{2}的函数解析式为y= -x+4$.
(1)求直线$l_{1}$的函数解析式;
(2)点P是直线$l_{1}$上的一个动点,当$△ABP$的面积为3时,求点P的坐标.

答案： 6.解:
(1)
∵点C(m,m)在直线y=-x+4上,
∴-m+4=m,解得m=2.
∴C(2,2).设直线l₁的函数解析式为y=kx+b,把A(-2,0),C(2,2)代入得{-2k+b=0,2k+b=2,解得{k=1/2,b=1.
∴直线l₁的函数解析式为y=1/2x+1.
(2)
∵P是直线l₁上的一个动点,
∴设P(x,1/2x+1).易得B(4,0),
∴AB=4-(-2)=6.又
∵△ABP面积为3,
∴1/2×6×|1/2x+1|=3,解得x=0或x=-4.当x=0时,1/2x+1=1;当x=-4时,1/2x+1=-1.
∴点P的坐标为(0,1)或(-4,-1).