2025年时习之暑假衔接八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
实践活动二
在学习完特殊的平行四边形之后,老师在数学活动课上展示了下面一道与平行四边形有关的折叠题:
[问题情境]
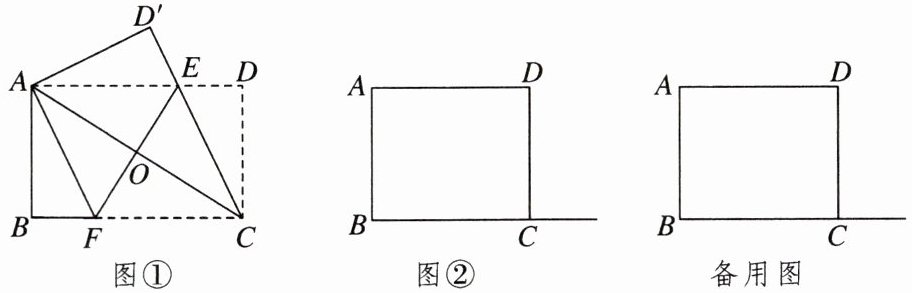
如图①,将矩形纸片ABCD沿直线EF折叠,使得点C与点A重合,点D落在点D'的位置,连接EC,AF,AC,线段AC交EF于点O。
[独立思考]
(1)△AEF是______三角形(按边分类);
[实践探究]
(2)请判断四边形AFCE的形状,并说明理由;
[拓展延伸]
(3)如图②,矩形纸片ABCD,AB= 5,BC= 6,若点M为射线BC上一点,将△ABM沿着直线AM折叠,折叠后点B的对应点为B',当点B'恰好落在BC的垂直平分线上时,请直接写出BM的长。
在学习完特殊的平行四边形之后,老师在数学活动课上展示了下面一道与平行四边形有关的折叠题:
[问题情境]
如图①,将矩形纸片ABCD沿直线EF折叠,使得点C与点A重合,点D落在点D'的位置,连接EC,AF,AC,线段AC交EF于点O。
[独立思考]
(1)△AEF是______三角形(按边分类);
[实践探究]
(2)请判断四边形AFCE的形状,并说明理由;
[拓展延伸]
(3)如图②,矩形纸片ABCD,AB= 5,BC= 6,若点M为射线BC上一点,将△ABM沿着直线AM折叠,折叠后点B的对应点为B',当点B'恰好落在BC的垂直平分线上时,请直接写出BM的长。

答案:
(1)等腰
(2)四边形AFCE是菱形,理由如下:
∵四边形ABCD 是矩形,
∴AD//BC,即AE//FC.
∴∠AEF=∠CFE.根据折叠的性质可知∠CFE=∠AFE,CF=AF,
∴∠AEF=∠AFE,
∴AE=AF.
∴AE=FC.
∴四边形AFCE是平行四边形.又
∵AE=AF,
∴四边形AFCE是菱形.
(3)BM的长为$\frac{5}{3}$或15. 点拨:设BC边的垂直平分线分别交AD,BC于点E,F.
①如图a,当点M在线段BC上时,
∵四边形ABCD是矩形,EF垂直平分BC,
∴四边形ABFE是矩形.
∴∠AEB'=90°,∠MFB'=90°,AE=BF=$\frac{1}{2}$BC=3,EF=AB=5.根据折叠的性质可知AB'=AB=5,B'M=BM,
∴EB'=$\sqrt{AB'^2 - AE^2}=\sqrt{5^2 - 3^2}=4$.
∴B'F=1.设BM=B'M=x,则MF=3−x.在Rt△B'MF 中,B'M²=MF²+B'F²,
∴x²=(3−x)²+1²,解得x=$\frac{5}{3}$.
∴BM=$\frac{5}{3}$.
②如图b,当点M在线段BC的延长线上时,
∵∠AEF=90°,∠MFB'=90°,AE=BF=3,EF=AB=5,根据折叠的性质可知AB'=AB=5,BM=B'M,
∴EB'=$\sqrt{AB'^2 - AE^2}=\sqrt{5^2 - 3^2}=4$.
∴B'F=EB'+EF=4+5=9.设BM=B'M=x,则MF=x−3.在Rt△B'MF 中,B'M²=B'F²+MF²,
∴x²=9²+(x−3)²,解得x=15.
∴BM=15.综上所述,BM的长为$\frac{5}{3}$或15.
(1)等腰
(2)四边形AFCE是菱形,理由如下:
∵四边形ABCD 是矩形,
∴AD//BC,即AE//FC.
∴∠AEF=∠CFE.根据折叠的性质可知∠CFE=∠AFE,CF=AF,
∴∠AEF=∠AFE,
∴AE=AF.
∴AE=FC.
∴四边形AFCE是平行四边形.又
∵AE=AF,
∴四边形AFCE是菱形.
(3)BM的长为$\frac{5}{3}$或15. 点拨:设BC边的垂直平分线分别交AD,BC于点E,F.
①如图a,当点M在线段BC上时,
∵四边形ABCD是矩形,EF垂直平分BC,
∴四边形ABFE是矩形.
∴∠AEB'=90°,∠MFB'=90°,AE=BF=$\frac{1}{2}$BC=3,EF=AB=5.根据折叠的性质可知AB'=AB=5,B'M=BM,
∴EB'=$\sqrt{AB'^2 - AE^2}=\sqrt{5^2 - 3^2}=4$.
∴B'F=1.设BM=B'M=x,则MF=3−x.在Rt△B'MF 中,B'M²=MF²+B'F²,
∴x²=(3−x)²+1²,解得x=$\frac{5}{3}$.
∴BM=$\frac{5}{3}$.
②如图b,当点M在线段BC的延长线上时,
∵∠AEF=90°,∠MFB'=90°,AE=BF=3,EF=AB=5,根据折叠的性质可知AB'=AB=5,BM=B'M,
∴EB'=$\sqrt{AB'^2 - AE^2}=\sqrt{5^2 - 3^2}=4$.
∴B'F=EB'+EF=4+5=9.设BM=B'M=x,则MF=x−3.在Rt△B'MF 中,B'M²=B'F²+MF²,
∴x²=9²+(x−3)²,解得x=15.
∴BM=15.综上所述,BM的长为$\frac{5}{3}$或15.
查看更多完整答案,请扫码查看


