《2025年时习之暑假衔接八年级数学人教版》

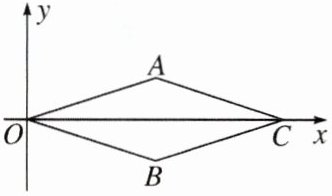
1. 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是 ( )

A.(3,1)

B.(3,-1)
C.(1,-3)
D.(1,3)

答案： B

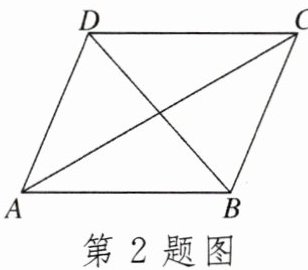
2. 如图,下列条件中不能使□ABCD成为菱形的是 ( )

A.AB= BC
B.AC⊥BD
C.∠ADB= ∠CDB
D.AD//BC

答案： D

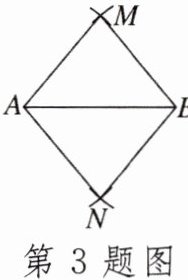
3. 如图,AB= 6cm,分别以A,B为圆心,5cm长为半径画弧,两弧相交于M,N两点。连接AM,BM,AN,BN,则四边形AMBN的面积为$______cm^2。$

答案： 24

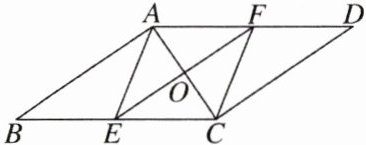
4. 如图,在□ABCD中,O为AC的中点,点E,F分别在BC,AD上,EF经过点O,AE= AF。
(1)求证：四边形AECF为菱形；
(2)若E为BC的中点,AE= 3,AC= 4,求AB的长。

答案：
(1)证明:
∵四边形ABCD是平行四边形,
∴AD//BC.
∴∠OAF=∠OCE.
∵O为AC的中点,
∴OA=OC.在△AOF和△COE中,$\left\{\begin{array}{l} ∠OAF=∠OCE,\\ OA=OC,\\ ∠AOF=∠COE,\end{array}\right. $
∴△AOF≌△COE(ASA).
∴AF=CE.
∵AF//CE,
∴四边形AECF是平行四边形.
∵AE=AF,
∴四边形AECF是菱形.
(2)解:
∵四边形AECF是菱形,AE=3,AC=4,
∴CE=AE=3.
∵E为BC的中点,
∴BE=CE=AE=3.
∴BC=2BE=6,∠EAC=∠ECA,∠EAB=∠B.
∴∠BAC=∠EAC+∠EAB=$\frac{1}{2}×180°=90°$.
∴AB=$\sqrt{BC^2-AC^2}=\sqrt{6^2-4^2}=2\sqrt{5}$.
∴AB的长是$2\sqrt{5}$.