《2025年通城学典小学毕业考试试题分类精粹数学江苏专版》

48. (2024·南通海安)将A、B两种积木没有规律地横排拼接成一个大的长方体(如图),已知大长方体的总长是36厘米,一共用了10块积木。A、B两种积木各用了多少块?

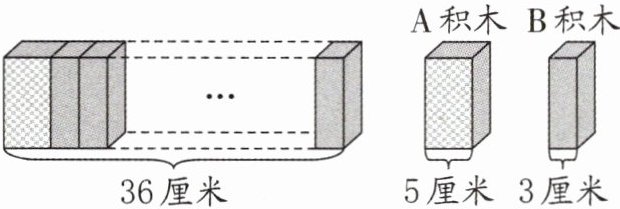
答案： B积木:(5×十-36)÷(5-3)=7(块)A积木:10-7=3(块)

49. (2024·南京栖霞区)复习课上,栖栖发现:在正方形中画一个最大的圆,无论正方形的边长怎么变化,正方形的周长与圆的周长比都是4:π,正方形的面积与圆的面积比也都是4:π。
(1)你认为栖栖的发现正确吗? 请举例说明。

(2)研究中栖栖还发现,在立体图形中也同样存在这种关系。把上、下底面是正方形的长方体削成一个最大的圆柱,这时长方体的体积与圆柱的体积比也是4:π。根据这一发现,如果把如图所示的这根体积是2000立方厘米的长方体木料削成一个最大的圆柱,那么圆柱的体积是多少立方厘米?

答案：
(1)我认为栖栖的发现正确 举例不唯一,如假设正方形的边长是4厘米。 正方形的周长:4×4=16(厘米) 圆的周长:$π×4=4π$(厘米)它们的周长比:$16:4π=4:π$ 正方形的面积:4×4=16(平方厘米) 圆的面积:$π×(4÷2)^{2}=4π$(平方厘米) 它们的面积比:$16:4π=4:π$
(2)$2000÷4×π=500π$(立方厘米)

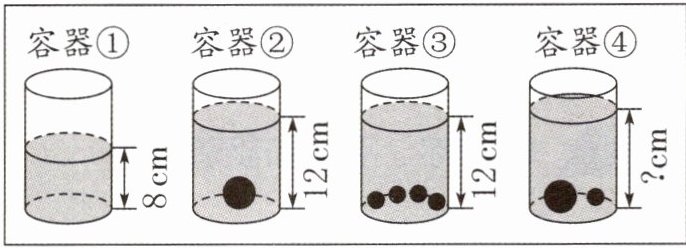
50. (2024·盐城阜宁)有四个完全相同的圆柱形容器,先装入同样多的水,再分别往容器②、③、④中放入大、小两种规格的钢球,水面高度变化如图所示。现在容器④中的水面高度是(13)cm。

答案： 13 【解析】观察题图②可知,一个大钢球放入水中,水面升高了12-8=4(cm);观察题图③可知,四个小钢球放入水中,水面升高了12-8=4(cm),所以一个小钢球放入水中,水面会升高1 cm,题图④中放入了一个大钢球和一个小钢球,水面会升高5 cm。

51. (2024·宿迁宿豫区)“数学实验”是数学学习的一种重要方式。在数学实验课上,王老师和同学们合作测量一些相同螺丝钉的体积,他们进行了如下实验:
① 小亮准备了一个圆柱形玻璃杯,从里面量,底面直径是4厘米,高是14厘米。
② 小明往玻璃杯里注入一些水,水的高度是8厘米。
③ 小芳把40枚相同的螺丝钉放入玻璃杯(螺丝钉浸没在水中),测得此时水的高度与水面离杯口的距离之比是5:2。
根据上面的信息,计算出1枚螺丝钉的体积。

答案： $14×\frac {5}{5+2}=10$(厘米)3.14×(4÷2)²×(10-8)=25.12(立方厘米)25.12÷40=0.628(立方厘米)