《2025年通城学典小学毕业考试试题分类精粹数学江苏专版》

12. (2024·南通海安)甲、乙两车同时从A、B两地出发,相向而行。当两车相遇时,甲车行驶了全程的$\frac {3}{7}$,乙车比甲车多行驶70千米。A、B两地相距多少千米?

答案： $70\÷(1-\frac{3}{7}-\frac{3}{7})=490$(千米)

13. (2024·盐城阜宁)下面是从小红家到小明家的路线示意图,正中间是公园。
小红家 公园 小明家

一天,小红和小明同时从自己家出发,相向而行,小红每分钟走90米,小明每分钟走120米,经过8分钟两人相遇。
(1)在图上标出小红和小明相遇地点的大概位置,并说明理由。
(2)小红和小明两家相距多少米?

答案： （1）小红家 公园 小明家
理由:小明与小红的速度比是$4:3$,所以经过8分钟,小明与小红走的路程比为$4:3$。（合理即可）
（2）$(120+90)×8=1680$(米)

14. (2023·常州溧阳)如图,小明骑自行车从家出发,经图书馆去表哥家。小明骑自行车每分钟行0.3千米,表哥骑自行车每分钟行0.36千米。

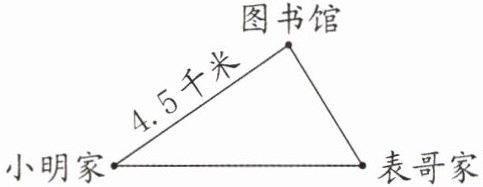
(1)从图书馆骑到表哥家的时间比从家骑到图书馆少5分钟,从图书馆到表哥家有多少千米?
(2)到达表哥家后,小明和表哥同时从表哥家出发直接去小明家,表哥到达小明家后立即返回,在离小明家0.48千米的地方遇到了小明。此时,表哥骑了多少分钟?

答案： （1）$4.5\÷0.3=15$(分) $0.3×(15-5)=3$(千米)
（2）$0.48×2\÷(0.36-0.3)=16$(分)

15. (2023·无锡江阴)甲、乙两车的速度比是8:5,它们同时从A、B两地开出,相向而行,经过2小时在距离中点36千米处相遇。A、B两地相距多少千米?

答案： $36×2\÷(8-5)×(8+5)=312$(千米)

16. (2024·苏州常熟)道路限速监控管理的一种方式是采用“区间测速”,就是测算出汽车在某一区间行驶的平均速度,如果超过了该路段的最高限速即判为超速。

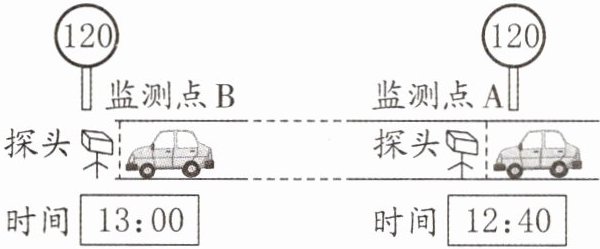
(1)若一辆轿车通过两个监测点的时间如图,监测点A、B相距45千米,采用“区间测速”时,请通过计算说明这辆轿车在该路段会不会超速。
(2)若一辆货车以100千米/时的速度匀速通过监测点A、B之间的这段路程,则它需要多少分钟?

答案： （1）13时-12时40分=20分 20分=$\frac{1}{3}$时
$45\÷\frac{1}{3}=135$(千米/时) $135＞120$ 会超速
（2）$45\÷100=0.45$(时) $0.45$时=27分