第118页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
1. (2024·南通通州区)古希腊著名的毕达哥拉斯学派对“三角形数、正方形数”等有所研究。
(1) 他们把1、3、6、10、15……这样的数称为“三角形数”(如图),第6个“三角形数”是(
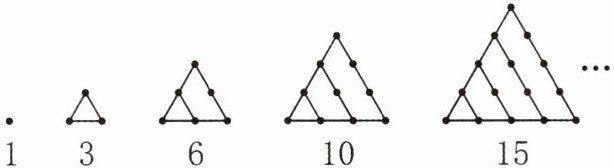
(2) 他们把1、4、9、16、25……这样的数称为“正方形数”(如图),第n个“正方形数”是(
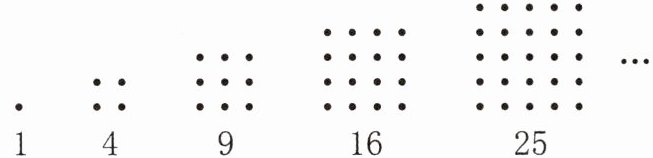
(3) 如果用一条斜线把“正方形数”分成了两部分(如图)。可以发现:任何一个大于1的“正方形数”都可以看成两个相邻的“三角形数”的和。以此类推,第ⓝ幅图为(
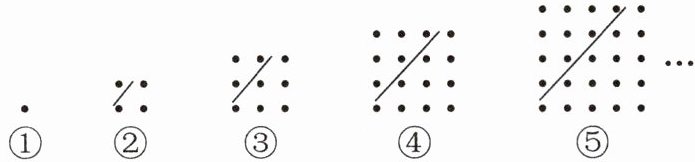
(1) 他们把1、3、6、10、15……这样的数称为“三角形数”(如图),第6个“三角形数”是(
21
);第n个“三角形数”是($\frac{n(n+1)}{2}$
)。
(2) 他们把1、4、9、16、25……这样的数称为“正方形数”(如图),第n个“正方形数”是(
$n^2$
)。
(3) 如果用一条斜线把“正方形数”分成了两部分(如图)。可以发现:任何一个大于1的“正方形数”都可以看成两个相邻的“三角形数”的和。以此类推,第ⓝ幅图为(
$n^2$
)= ($\frac{n(n-1)}{2}$
)+($\frac{n(n+1)}{2}$
)。
答案:
1.
(1)21 $\frac{n(n+1)}{2}$
(2)$n^2$
(3)$n^2$ $\frac{n(n-1)}{2}$ $\frac{n(n+1)}{2}$
(1)21 $\frac{n(n+1)}{2}$
(2)$n^2$
(3)$n^2$ $\frac{n(n-1)}{2}$ $\frac{n(n+1)}{2}$
2. (2024·宜春袁州区)按规律填空:1、3、6、10、15、(
21
)、28、36、(45
)。
答案:
21 45
3. (2024·南通如东)有这样一串有规律的数:1、4、7、10、13、16……
(1) 从前往后数,第10个数是(
探索规律
相应“答案与解析”见P26
目标
(2) 从前往后数,100是这串数中第(
(1) 从前往后数,第10个数是(
28
),第n个数是(3n-2
)。探索规律
相应“答案与解析”见P26
目标
(2) 从前往后数,100是这串数中第(
34
)个数,在前100个数中,有(50
)个奇数。
答案:
3.
(1)28 $3n-2$
(2)34 50
(1)28 $3n-2$
(2)34 50
4. (2023·扬州江都区)小华在计算$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}+8^{2}+13^{2}$这样的算式时,想到用“数形结合”的方法来探究,他以这组数中各个数作为正方形的边长构建正方形,再拼成长方形来研究,过程如下:
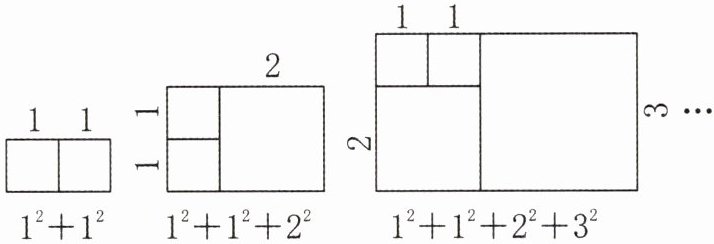
(1) 观察图形和算式,把下面的算式补充完整。
$1^{2}+1^{2}= 1×2$
$1^{2}+1^{2}+2^{2}= 2×3$
$1^{2}+1^{2}+2^{2}+3^{2}= 3×5$
$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}= $(
$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}+8^{2}= $(
$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}+8^{2}+13^{2}= $(
(2) 若按此规律继续拼长方形,则第10个长方形的面积是(

(1) 观察图形和算式,把下面的算式补充完整。
$1^{2}+1^{2}= 1×2$
$1^{2}+1^{2}+2^{2}= 2×3$
$1^{2}+1^{2}+2^{2}+3^{2}= 3×5$
$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}= $(
5
)×(8
)$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}+8^{2}= $(
8
)×(13
)$1^{2}+1^{2}+2^{2}+3^{2}+5^{2}+8^{2}+13^{2}= $(
13
)×(21
)(2) 若按此规律继续拼长方形,则第10个长方形的面积是(
12816
);若长方形的面积是714,则算式为($1^2+1^2+2^2+3^2+5^2+8^2+13^2+21^2$
)。
答案:
4.
(1)5 8 8 13 13 21
(2)12816 $1^2+1^2+2^2+3^2+5^2+8^2+13^2+21^2$
(1)5 8 8 13 13 21
(2)12816 $1^2+1^2+2^2+3^2+5^2+8^2+13^2+21^2$
$3×4-1= 11$
$33×34-11= 1111$
$333×334-111= 111111$
$3333×3334-1111= $
$33×34-11= 1111$
$333×334-111= 111111$
$3333×3334-1111= $
11111111
答案:
11111111
查看更多完整答案,请扫码查看


