《2025年通城学典小学毕业考试试题分类精粹数学江苏专版》

14. (2023·合肥瑶海区)善于退,足够的退,退到最原始而又不失重要性的地方,这是学好数学的一个诀窍。这里的“退”,含义很丰富,意思是说,在面对疑难问题时,可以将问题退到最简单的状态探究其中隐含的规律。你能用“退”的方法从简单处想起,探索规律,解决下面这个问题吗?
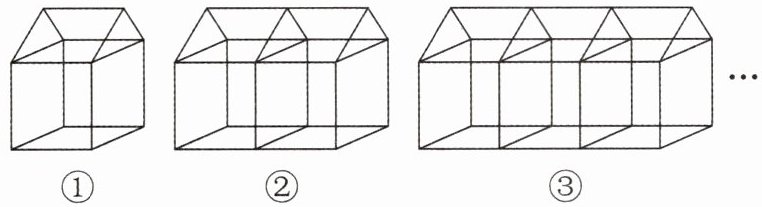
如图所示为由钢管搭建的帐篷,先仔细观察图,再填一填。

395011n+6

答案： 39　50　$11n+6$

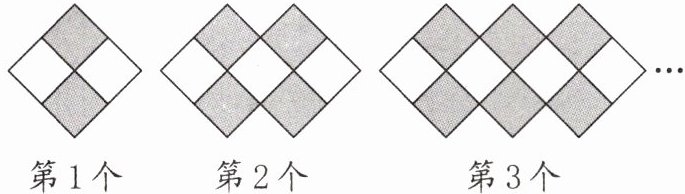
15. (2023·杭州淳安)4个边长为1cm的小正方形组成图形。下面这一列图形由重叠而成。按这样的方式重叠,第5个图形的周长是(24)cm。

答案： 24

16. (2023·连云港灌云)如图所示为用☆按规律拼成的图案,第n个图案中有(3n+1)颗☆。

答案： $3n+1$

17. (2024·南通海安)数学中规定：连接多边形任意两个不相邻顶点的线段叫作多边形的对角线。

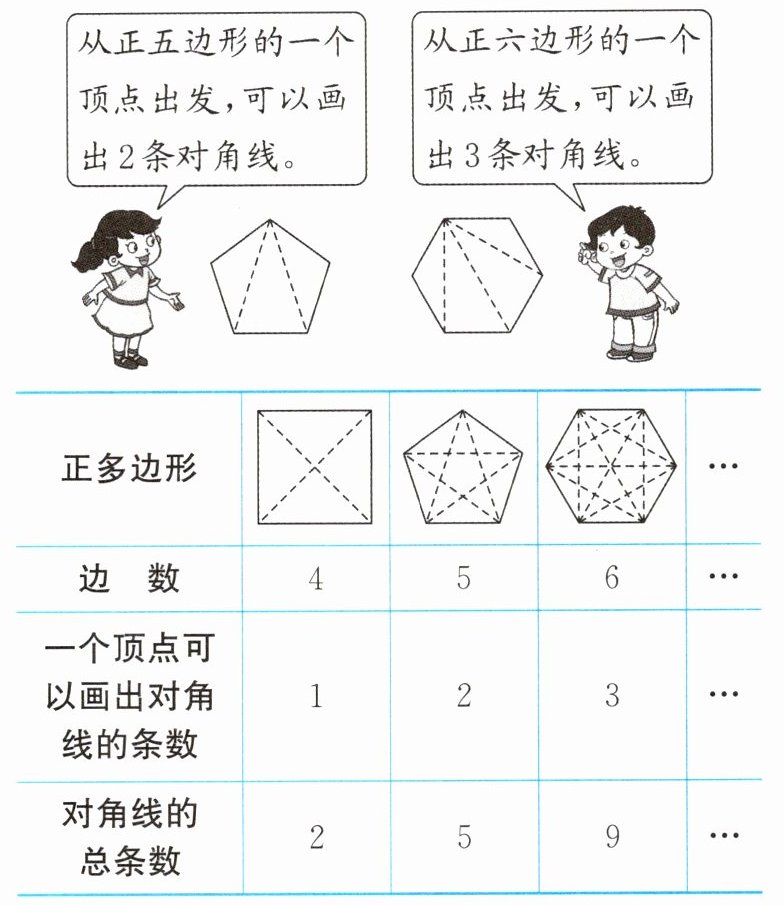
聪聪是个喜欢思考的学生,他发现正多边形的对角线的总条数和正多边形的边数存在某种规律(如上表)。照这样的规律,正七边形共有(14)条对角线,正n边形共有($\frac{n(n-3)}{2}$)条对角线。

答案： 14　$\frac{n(n-3)}{2}$

18. (2024·南通通州区)用96cm长的绳子在桌面上摆出正方形,先把这根绳子摆成1个正方形,再把这根绳子摆成2个正方形、3个正方形、4个正方形……

(1) 正方形的个数与每个正方形边长之间的关系如下：
观察上表,可知$xy=$(24)。
(2) 正方形的个数与所摆图形顶点个数的关系如下：

当正方形的个数是x时,顶点个数是(3x+1)；当摆出的图形共有100个顶点时,共摆了(33)个正方形。

答案： 18.
(1)24　
(2)$3x+1$　33