第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
43. (2024·苏州常熟)菁菁用完全相同的圆柱进行三种不同的切分(如图)。已知圆柱的底面直径是4厘米。第一种切分方式表面积会增加(
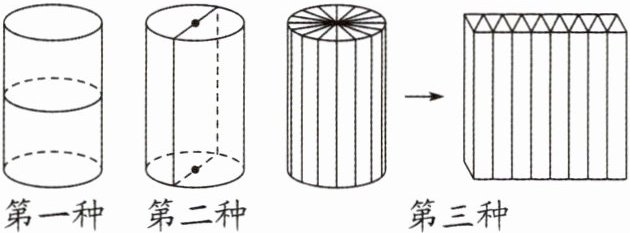
25.12
)平方厘米,第二种切分方式表面积会增加48平方厘米,第三种切分方式表面积会增加(24
)平方厘米。无论怎样切分,这个圆柱的体积都是(75.36
)立方厘米。
答案:
25.12 24 75.36
44. (2024·苏州常熟)如图,一个圆锥的高是3厘米,沿着它的高平均切成两部分,表面积增加12平方厘米,原来圆锥的底面直径是(
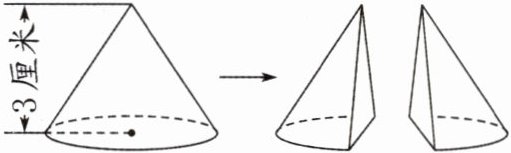
4
)厘米,体积是(12.56
)立方厘米。
答案:
4 12.56
45. (2024·南通通州区)等底等高的图形在数学知识的学习中有着重要的作用。
(1)把一个圆柱平均分成若干份,拼成一个近似的长方体(如图),长方体的宽是2分米,高是3分米,长方体的长是(
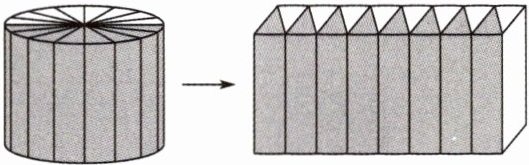
(2)如果一个圆柱和圆锥等底等高,同时圆柱比圆锥的体积多50立方分米,那么这个圆柱的体积是(
(3)等底等高的平行四边形和三角形,如果它们的面积之和是36平方厘米,它们的底都是10厘米,那么它们的高都是(
(1)把一个圆柱平均分成若干份,拼成一个近似的长方体(如图),长方体的宽是2分米,高是3分米,长方体的长是(
6.28
)分米,圆柱的体积是(37.68
)立方分米。
(2)如果一个圆柱和圆锥等底等高,同时圆柱比圆锥的体积多50立方分米,那么这个圆柱的体积是(
75
)立方分米。(3)等底等高的平行四边形和三角形,如果它们的面积之和是36平方厘米,它们的底都是10厘米,那么它们的高都是(
2.4
)厘米。
答案:
(1)6.28 37.68
(2)75
(3)2.4
(1)6.28 37.68
(2)75
(3)2.4
46. 选择。
(1) (2024·连云港赣榆区)如图,把圆柱切拼成一个近似的长方体,下面的说法中,正确的是(
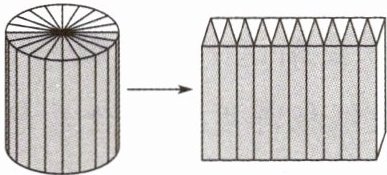
A. 表面积不变,体积也不变
B. 表面积变小,体积不变
C. 表面积变大,体积不变
D. 表面积变大,体积也变大
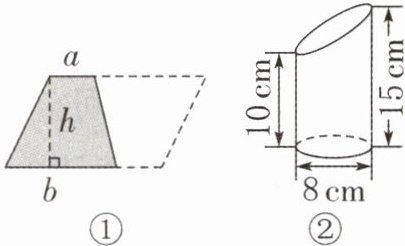
(2) (2024·南通海门区)如图①,用两个完全相同的梯形拼成平行四边形,推导出了梯形的面积计算公式。用这样的思路,可以求出如图②所示的立体图形的体积是(
A. 100
B. 160π
C. 200π
D. 240π
(1) (2024·连云港赣榆区)如图,把圆柱切拼成一个近似的长方体,下面的说法中,正确的是(
C
)。
A. 表面积不变,体积也不变
B. 表面积变小,体积不变
C. 表面积变大,体积不变
D. 表面积变大,体积也变大
(2) (2024·南通海门区)如图①,用两个完全相同的梯形拼成平行四边形,推导出了梯形的面积计算公式。用这样的思路,可以求出如图②所示的立体图形的体积是(
C
)$cm^3。$A. 100

B. 160π
C. 200π
D. 240π
答案:
(1)C
(2)C
(1)C
(2)C
47. (2024·常州溧阳)陈爷爷家的老屋要翻建,从老屋上拆下一根圆柱形的木料(如图)。
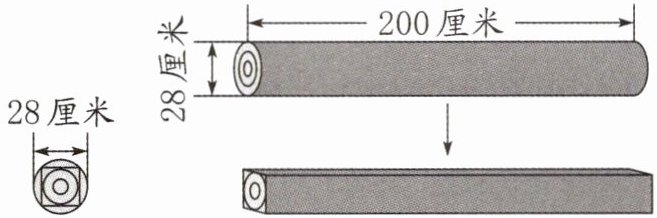
(1)这根木料的侧面有一层斑驳的红漆,原来刷红漆的部分有多少平方厘米?
(2)现在要把这根木料加工成方木(横截面为正方形),这根方木的体积最大是多少立方厘米? 合多少立方分米?

(1)这根木料的侧面有一层斑驳的红漆,原来刷红漆的部分有多少平方厘米?
(2)现在要把这根木料加工成方木(横截面为正方形),这根方木的体积最大是多少立方厘米? 合多少立方分米?
答案:
(1)3.14×28×200=17584(平方厘米)
(2)28×(28÷2)÷
(3)2×2×200=78400(立方厘米)78400立方厘米=78.4立方分米【解析】方木的最大体积是以200厘米为高,对角线是28厘米的正方形为底面的长方体的体积。
(1)3.14×28×200=17584(平方厘米)
(2)28×(28÷2)÷
(3)2×2×200=78400(立方厘米)78400立方厘米=78.4立方分米【解析】方木的最大体积是以200厘米为高,对角线是28厘米的正方形为底面的长方体的体积。
查看更多完整答案,请扫码查看


