第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
(3)(2024·苏州张家港)下面的4个图形中,面积最大的是(
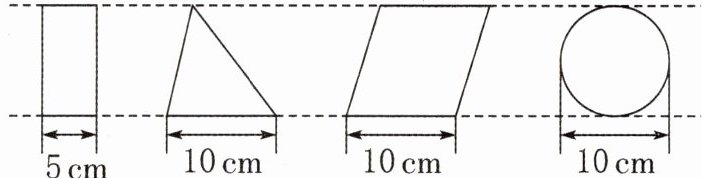
A.长方形
B.三角形
C.平行四边形
D.圆
C
)。
A.长方形
B.三角形
C.平行四边形
D.圆
答案:
C
一堆钢管按左下图所示的方式堆放,最上层有9根,最下层有18根,共10层,这堆钢管一共有(
A.126
B.128
C.133
D.135
D
)根。A.126
B.128
C.133
D.135
答案:
D
(5)(2024·无锡江阴)如右上图所示为一张长方形纸,宽为a,长是宽的2倍。在这张长方形纸中剪去一个半圆,那么剩下部分的周长是(

A.$6a+\frac{1}{2}\pi a$
B.$5a+\frac{1}{2}\pi a$
C.$2a^{2}-\frac{1}{8}\pi a^{2}$
D.$2a^{2}-\frac{1}{4}\pi a^{2}$
B
)。
A.$6a+\frac{1}{2}\pi a$
B.$5a+\frac{1}{2}\pi a$
C.$2a^{2}-\frac{1}{8}\pi a^{2}$
D.$2a^{2}-\frac{1}{4}\pi a^{2}$
答案:
B
(6)(2024·南京江北新区)如左下图,在三角形ABC中,边BC和它对应的高都是4厘米。如果把点A和点C同时以2厘米/秒的速度向右平移,就形成一个梯形,经过3秒,形成的梯形的面积是(
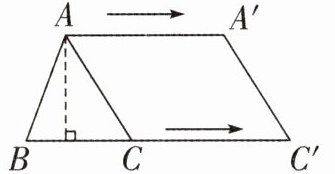
A.64
B.40
C.32
D.20
C
)平方厘米。
A.64
B.40
C.32
D.20
答案:
C
(7)(2024·宿迁宿豫区)如右上图,正方形的面积是10平方厘米,圆的面积是(

A.$5\pi$
B.$2.5\pi$
C.$10\pi$
D.$20\pi$
A
)平方厘米。
A.$5\pi$
B.$2.5\pi$
C.$10\pi$
D.$20\pi$
答案:
A
(8)(2023·平顶山新华区)下面是梯形ABCD转化成三角形ADE的过程,若梯形ABCD的面积是$54cm^{2}$,高是9cm,则三角形ADE的底DE的长是(
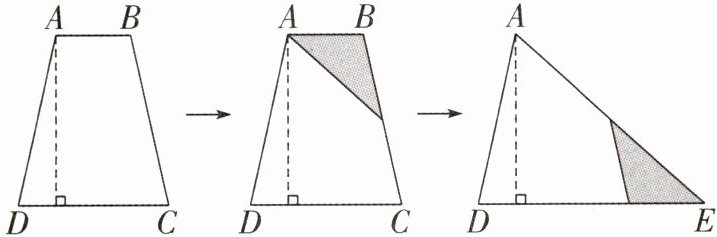
A.3
B.6
C.12
D.16
C
)cm。
A.3
B.6
C.12
D.16
答案:
C
(9)(2024·泰州泰兴)如左下图,平行四边形ABCD的面积是$10cm^{2}$,则圆的面积是(
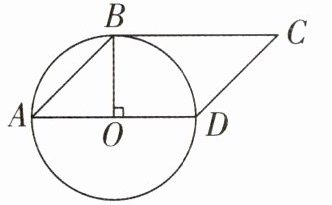
A.10
B.15.7
C.20
D.31.4
B
)$cm^{2}$。
A.10
B.15.7
C.20
D.31.4
答案:
B
(10)(2024·吉安井冈山)如右上图,用8个完全相同的小长方形可以拼成一个大长方形,每个小长方形的面积是(

A.96
B.75
C.50
D.64
B
)$cm^{2}$。
A.96
B.75
C.50
D.64
答案:
B
(11)(2023·南京江北新区)我国古代数学家刘徽利用出入相补原理来计算平面图形的面积。例如:把如图所示的三角形分割、移补成长方形,保持面积不变,来计算它的面积。该图求三角形面积的方法是(
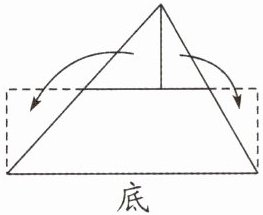
A.(底$÷$2)$×$高
B.底$×$高
C.底$×高÷$2
D.底$×$(高$÷$2)
D
)。
A.(底$÷$2)$×$高
B.底$×$高
C.底$×高÷$2
D.底$×$(高$÷$2)
答案:
D
(12)(2023·无锡锡山区)在一幅比例尺为1:300的零件图上,甲、乙两个圆的直径之比为3:5,那么它们的实际面积之比为(
A.3:5
B.9:25
C.1:300
D.1:600
B
)。A.3:5
B.9:25
C.1:300
D.1:600
答案:
B
查看更多完整答案,请扫码查看


