《2025年通城学典小学毕业考试试题分类精粹数学江苏专版》

29. (2024·南京建邺区)求组合图形的体积。

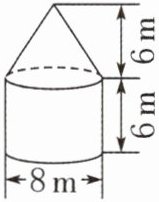
答案： $3.14×(8÷2)^{2}×6×(1+\frac {1}{3})=401.92(m^{3})$

30. (2024·苏州太仓)如图,一个密闭的容器是由圆柱和圆锥组成的,圆柱和圆锥的高分别为12厘米、9厘米,容器内的水面高8厘米。如果将这个容器倒过来放置,那么从圆锥的顶点到水面的距离是多少厘米? (容器壁的厚度忽略不计)

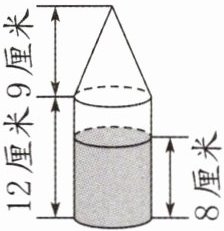
答案： $S×8-\frac {1}{3}×S×9=5S$(立方厘米)$h=V÷S=5S÷S=5$(厘米) 9+5=14(厘米)【解析】圆柱与圆锥的底面积相等,将容器倒过来放置,则水的体积比圆锥形容器的容积多$S×8-\frac {1}{3}×S×9=5S$(立方厘米),根据多的体积与圆柱的底面积求出倒置后水在圆柱形容器中的高,最后将圆锥形容器中水的高度加上圆柱形容器中水的高度就是所求结果。

31. (2024·宿迁泗洪)一个圆锥形沙堆,高2米,紧绕沙堆走一圈至少要走18.84米。
(1)如果1立方米沙子的质量为1.4吨,那么这堆沙子的质量为多少吨?
(2)用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?

答案：
(1)$\frac {1}{3}×3.14×(18.84÷3.14÷2)^{2}×2=18.84$(立方米) 18.84×1.4=26.376(吨)
(2)18.84÷(7.5×4)=0.628(米)0.628米=62.8厘米

32. (2024·扬州广陵区)沙漏是我国古代一种计量时间的器具,它是根据流沙从一个容器漏到另一个容器的数量来计量时间的,如图所示为一个沙漏计量时间的情况。此时沙漏上部容器中沙子的体积是多少立方厘米? 现在下部容器中沙子的体积是31.4立方厘米,如果再过1分钟,沙漏上部容器中的沙子可以全部漏到下部容器中,那么现在下部容器中的沙子已经计量了多少分钟? (容器壁的厚度忽略不计)

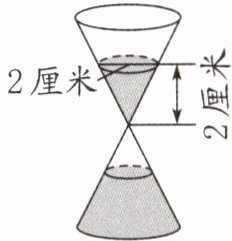
答案： $\frac {1}{3}×3.14×(2÷2)^{2}×2=\frac {157}{75}$(立方厘米)$31.4÷\frac {157}{75}=15$(分)

33. (2024·扬州高邮)一个无盖的长方体玻璃水槽,长5分米,宽4分米,高4分米。(玻璃的厚度忽略不计)
(1)做这个水槽至少需要玻璃多少平方分米? (损耗忽略不计)
(2)在该空水槽里注入76升水,水深多少分米?
(3)再往水里放入一个圆锥形金属件,这时水满并溢出2升。已知这个圆锥形金属件的高是3分米,则它的底面积是多少平方分米?

答案：
(1)5×4+(5×4+4×4)×2=92(平方分米)
(2)76升=76立方分米 76÷(5×4)=3.8(分米)
(3)2升=2立方分米 5×4×4-76+2=6(立方分米)$6÷\frac {1}{3}÷3=6$(平方分米)

34. (2024·苏州张家港)陀螺是历史悠久的儿童玩具。如图所示的陀螺,上面是圆柱,下面是圆锥,且圆锥的高是圆柱高的$\frac{3}{4}。$

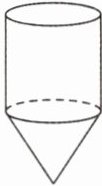
(1)已知圆柱的底面直径是8厘米,高是8厘米,这个陀螺的体积是多少立方厘米?
(2)如果要给这个陀螺做一个带盖长方体包装盒(硬纸板厚度及粘合处忽略不计),至少需要多少平方厘米的硬纸板?

答案：
(1)圆锥的高:$8×\frac {3}{4}=6$(厘米) 底面半径:8÷2=4(厘米) $3.14×4^{2}×8+\frac {1}{3}×3.14×4^{2}×6=502.4$(立方厘米)
(2)8×8×2+8×(8+6)×4=576(平方厘米)