第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
(5) (2024·无锡锡山区)如图,甲、乙是两个实心积木,甲和乙的体积之比是(
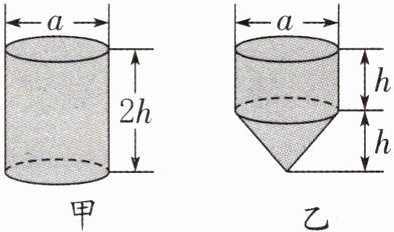
A.$3:1$
B.$3:2$
C.$4:1$
D.$4:3$
B
)。
A.$3:1$
B.$3:2$
C.$4:1$
D.$4:3$
答案:
B
(6) (2024·宁波宁海)如图,三角形 $AOC$与三角形 $BOD$形状相同、大小不同,在数学上把这样的两个三角形叫作“相似三角形”。已知 $AC:BD= 1:2$,$OC:OD= 1:2$,$OA:OB= 1:2$,则三角形 $AOC$与三角形 $BOD$的面积比是(
A.$1:2$
B.$1:3$
C.$1:4$
D.$1:8$
C
)。A.$1:2$
B.$1:3$
C.$1:4$
D.$1:8$
答案:
C
17. (2024·苏州太仓)(
3
)$÷5= 15:$(25
)$=\frac{(9
)}{15}= 0.6= $(60
)%
答案:
3 25 9 60
18. (2024·常州溧阳)$\frac{7}{20}= 28÷$(
80
)$=$(21
)$:60= $(35
)%
答案:
80 21 35
19. (2023·合肥蜀山区)(
8
)$÷20= 0.4= \frac{16}{(40
)}=$(40
)% $=$(2:5
)(填最简单的整数比)
答案:
8 40 40 2:5
20. (2023·洛阳孟津区)$m:n= \frac{
m
}{n
}= $m
$÷$n
($n$不为 0),比值相当于分数的值或除法算式中的商
。
答案:
$\frac{m}{n}$ m n 商
21. (2024·泰州泰兴)如果 $\frac{5a}{7}= \frac{3b}{4}$($a$、$b$均不为 0),那么 $a:b=$
21:20
(填最简单的整数比),$\frac{b}{a}=$$\frac{20}{21}$
。
答案:
21:20 $\frac{20}{21}$
22. (2023·青岛城阳区)已知甲、乙、丙三个数的平均数是 50,且甲 $ : $乙 $ : $丙 $ =2:3:5 $,则乙数是(
A.30
B.45
C.50
B
)。A.30
B.45
C.50
答案:
B
23. (2023·宿州萧县)一个长方体的棱长总和为 84 厘米,它的长、宽、高的比是 $4:2:1$。这个长方体的体积是多少立方厘米?
答案:
$84÷4÷(4+2+1)=3$(厘米)$4×3=12$(厘米) $2×3=6$(厘米)$1×3=3$(厘米) $12×6×3=216$(立方厘米)
24. (2023·淮安洪泽区)如图,在三角形中,$\angle1$与 $\angle2$的度数之比为 $3:1$,$\angle2$与 $\angle3$的度数之比为 $2:1$,则 $\angle1$、$\angle2$、$\angle3$分别是多少度?
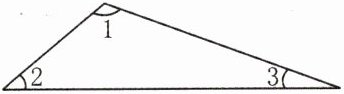

答案:
因为$\angle1:\angle2=3:1$,$\angle2:\angle3=2:1$,所以$\angle1:\angle2:\angle3=6:2:1$。所以$\angle1=180^{\circ}×\frac{6}{6+2+1}=120^{\circ}$,$\angle2=180^{\circ}×\frac{2}{6+2+1}=40^{\circ}$,$\angle3=180^{\circ}×\frac{1}{6+2+1}=20^{\circ}$
查看更多完整答案,请扫码查看


