《2025年通城学典小学毕业考试试题分类精粹数学江苏专版》

6. (2023·无锡梁溪区)数的计算中有一些有趣的对称形式,如$12×231= 132×21$；$23×352= 253×32$。现在有两个与此规律相同的等式,请完成填空。
$45×594=$495×54；若$63×3□6= ○×36$,则$○=$693。

答案： 495　54　693

$2= 1×2$
$2+4= 2×3$
$2+4+6= 3×4$
…
$2+4+6+8+10+12= $6×7

答案： 6　7

8. (2023·南通如东)先观察,再解决问题。
有这样一组有规律的算式：
第1层：$1+2= 3$；
第2层：$4+5+6= 7+8$；
第3层：$9+10+11+12= 13+14+15$；
第4层：$16+17+18+19+20= 21+22+23+24$；
第5层：$25+26+27+28+29+30= 31+32+33+34+35$；
…
(1) 我发现：每层的第1个数都正好等于层数的平方,如第7层的第1个数是49。
(2) 我发现：每层等号右边的数的个数都正好等于层数,如第7层等号右边一共有7个数。
(3) 请你列式计算出第7层等号左边的数的和。
$7^2=49$　$49+50+51+52+53+54+55+56=(49+56)×8÷2=420$

答案： 8.
(1)层数的平方　49　
(2)层数　7
(3)$7^2=49$　$49+50+51+52+53+54+55+56=(49+56)×8÷2=420$

9. (2024·苏州太仓)如图,按这样的规律,第四个图形中有(40)个白色三角形。

答案： 40

10. (2023·无锡锡山区)小妍用一些长为5厘米的小棒搭出了一组长(正)方体框架,如图所示为她搭的前三个框架,搭第1个框架需要12根小棒,搭第2个框架需要20根小棒,搭第3个框架需要28根小棒……照这样搭下去,小妍搭第7个框架需要(60)根小棒。若她想要用彩纸全包住她搭的第n个框架,则至少需要(100n+50)平方厘米的彩纸。

答案： 60　$100n+50$

11. (2023·南通海安)冬冬用吸管和图钉做三角形。(如图,圆点表示图钉,线段表示吸管)

(1) 做4个三角形需要(6)个图钉和(9)根吸管。
(2) 做a个三角形需要(a+2)个图钉和(2a+1)根吸管。

答案： 11.
(1)6　9　
(2)$a+2$　$2a+1$

12. (2024·无锡锡山区)探索规律。

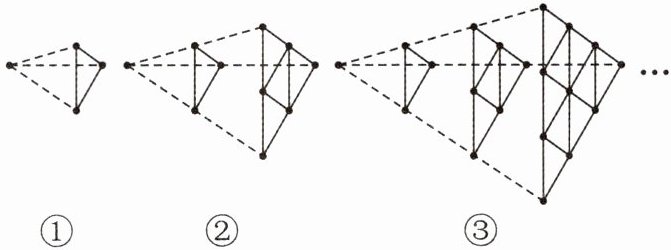
如图,图①中有4个点,按照这样的规律摆下去,图④比图③多了(15)个点,从图(⑥)(填序号)起,所用的点数超过70个。

答案： 15　⑥

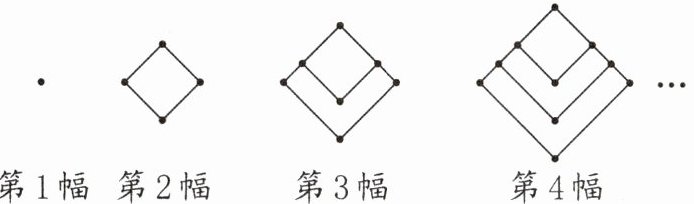
13. (2024·徐州泉山区)“数缺形时少直观,形少数时难入微”。观察每幅图中点数的变化规律,依次排列下去,第5幅图中有(13)个点,第n幅图中有($3n-2$)个点。

答案： 13　$3n-2$