第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
14. (2023·无锡江阴)若$\frac{x}{5}= \frac{8}{y}$($y$不为0),则$x和y$成(
反
)比例;若$x×3= y÷\frac{1}{7}$($x$、$y$均不为0),则$x和y$成(正
)比例。
答案:
反 正 【解析】由$\frac{x}{5}=\frac{8}{y}$(y不为0),得$xy = 40$(一定),所以x和y成反比例;由$x× 3=y÷ \frac{1}{7}$(x、y均不为0),得$\frac{x}{y}=\frac{7}{3}$(一定),所以x和y成正比例。
15. (2024·南京江北新区)如果$3A= 1.5B$($A$、$B$均不为0),那么$A和B$成(
正
)比例。
答案:
正
16. (2023·常州溧阳)明明发现学校有一个漏水的水龙头,他记录了这个水龙头的滴水情况,如下表:
|滴水量/毫升|15|30|45|60|75|…|
|时间/分|1|2|3|4|5|…|
(1) 滴水量和时间成(
(2) 明明在这个水龙头的下方放一个容积为7.65升的水桶,则(
|滴水量/毫升|15|30|45|60|75|…|
|时间/分|1|2|3|4|5|…|
(1) 滴水量和时间成(
正
)比例。(2) 明明在这个水龙头的下方放一个容积为7.65升的水桶,则(
8.5
)小时可以接满。
答案:
(1)正
(2)8.5 【解析】先进行单位换算,7.65升=7650毫升,所以接满需要$7650÷ 15=510$(分),510分=8.5时。
(1)正
(2)8.5 【解析】先进行单位换算,7.65升=7650毫升,所以接满需要$7650÷ 15=510$(分),510分=8.5时。
(1) 该火箭飞行的时间和路程成(
(2) 小伟在春季运动会60米赛跑项目中跑出了9秒的成绩,这个时间内该火箭飞行了(
正
)比例关系。(2) 小伟在春季运动会60米赛跑项目中跑出了9秒的成绩,这个时间内该火箭飞行了(
70.2
)千米。
答案:
(1)正
(2)70.2
(1)正
(2)70.2
18. (2023·淮安)下图描述了一个水池进水管打开后进水量的情况。
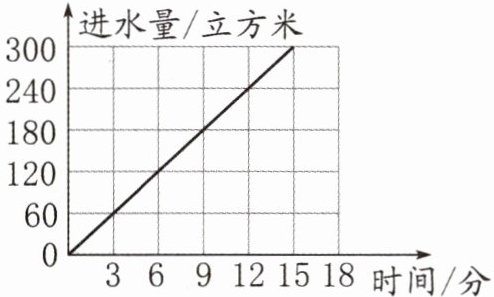
(1) 照这样的速度,要进水540立方米,需要(
(2) 该水池的进水量与时间成(

(1) 照这样的速度,要进水540立方米,需要(
27
)分钟;进水管打开1.5小时,进水量是(1800
)立方米。(2) 该水池的进水量与时间成(
正
)比例。
答案:
(1)27 1800
(2)正
(1)27 1800
(2)正
19. (2023·连云港赣榆区)在一次科学实验中,小丁记录了一壶水加热过程中水温的变化情况,并把它画成了下图。(整个过程在标准大气压下完成)
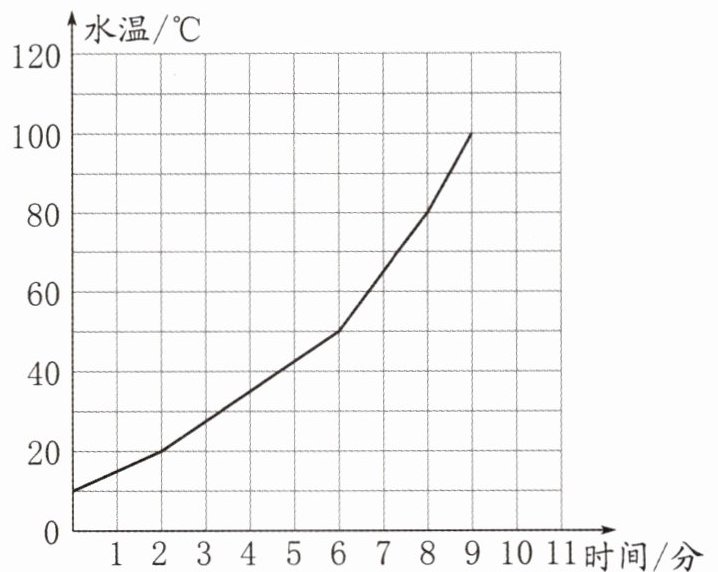
(1) 未加热时,水温是( )℃。
(2) 当水温上升到100℃,一共用了( )分钟。
(3) 根据整个加热过程中水温的变化情况,水温与时间( )比例关系。(填“成正”“成反”或“不成”)
(4) 如果继续加热到第11分钟,那么水温是( )℃。请将上图补充完整。

(1) 未加热时,水温是( )℃。
(2) 当水温上升到100℃,一共用了( )分钟。
(3) 根据整个加热过程中水温的变化情况,水温与时间( )比例关系。(填“成正”“成反”或“不成”)
(4) 如果继续加热到第11分钟,那么水温是( )℃。请将上图补充完整。
答案:
(1)10
(2)9
(3)不成
(4)100 如图所示
(1)10
(2)9
(3)不成
(4)100 如图所示

20. 判断。
(1) (2024·苏州吴江区)若$ab - 8 = 125$,则$a与b$成反比例关系。(
(2) (2023·钦州钦南区)若汽车的速度一定,则行驶的路程与所需的时间成反比例关系。(
(3) (2023·洛阳孟津区)路程和时间成正比例关系,单价和数量成反比例关系。(
(1) (2024·苏州吴江区)若$ab - 8 = 125$,则$a与b$成反比例关系。(
√
)(2) (2023·钦州钦南区)若汽车的速度一定,则行驶的路程与所需的时间成反比例关系。(
×
)(3) (2023·洛阳孟津区)路程和时间成正比例关系,单价和数量成反比例关系。(
×
)
答案:
(1)√ 【解析】$ab = 133$(一定),所以它们成反比例关系。
(2)× 【解析】由题意可知,$\frac{路程}{时间}=$速度(一定),所以路程与时间成正比例关系。
(3)× 【解析】题目中并未说明速度一定和总价一定,只有当速度一定时,路程和时间才成正比例关系,当总价一定时,单价和数量才成反比例关系。
(1)√ 【解析】$ab = 133$(一定),所以它们成反比例关系。
(2)× 【解析】由题意可知,$\frac{路程}{时间}=$速度(一定),所以路程与时间成正比例关系。
(3)× 【解析】题目中并未说明速度一定和总价一定,只有当速度一定时,路程和时间才成正比例关系,当总价一定时,单价和数量才成反比例关系。
(1) (2024·苏州常熟)下面各式中,$m与n$($m$、$n$均不为0)成反比例的是(
①$6:m = 5:n$ ②$m = n÷0.4$
③$\frac{3}{7}m= \frac{1}{n}$ ④$\frac{1}{m}×4= \frac{1}{4}× n$
A.①②
B.②③
C.③④
D.②④
C
)。①$6:m = 5:n$ ②$m = n÷0.4$
③$\frac{3}{7}m= \frac{1}{n}$ ④$\frac{1}{m}×4= \frac{1}{4}× n$
A.①②
B.②③
C.③④
D.②④
答案:
C
查看更多完整答案,请扫码查看


