《2025年全频道课时作业六年级数学下册人教版》

1. 填空。
(1)把一个圆柱削成一个最大的圆锥，圆锥体积是圆柱体积的(　　　)，削去部分的体积是圆锥体积的(　　　)，是圆柱体积的(　　　)。
(2)一个底面积是51 dm²、高是5 dm的圆柱形钢坯能熔铸成(　　　)个和它等底等高的圆锥，每个圆锥的体积是(　　　)dm³。
(3)向一个高15 cm的圆锥形容器中注满水后，再将水全部倒入一个与圆锥形容器等底等高的圆柱形容器中，这时圆柱形容器中的水高(　　　)cm。

答案：
(1)$\frac{1}{3}$　2倍　$\frac{2}{3}$　
(2)3　85　
(3)5

2. 根据图中已知条件求圆锥的体积。
　

答案：
(1)$\frac{1}{3}\times3.14\times2^{2}\times4.5 = 18.84(dm^{3})$　
(2)$\frac{1}{3}\times3.14\times(6\div2)^{2}\times4.5 = 42.39(dm^{3})$

3. 一个圆锥和一个圆柱的体积和高都相等，如果圆柱的底面积是5 cm²，那么圆锥的底面积是多少？

答案： 5×3 = 15(cm²)

4. 如图，四边形ABCD是直角梯形。以AB为轴，将梯形绕这条轴旋转一周，得到一个立体图形，它的体积是多少？(单位:cm)
　

答案： 3.14×3²×3+$\frac{1}{3}\times3.14\times3^{2}\times(6 - 3)=113.04(cm^{3})$

5. 李教授在实验室里把4 L水倒入下图的两个容器中，刚好都倒满。已知圆柱形和圆锥形容器的底面积和高都相等，则圆柱形容器和圆锥形容器的容积分别是多少升？
　

答案： 圆锥:4÷(3 + 1)=1(L)　圆柱:1×3 = 3(L)

6. [推理探究]一定时间内，降落在水平面上的水，在未经蒸发、渗漏、流失情况下所积的深度，称为降水量(通常以毫米为单位)。某地区的土地面积为45 km²，5月的一天日降水量为100 mm。这些水的15%大约能装满几个口径30 m、深10 m的圆锥形蓄水池？
　

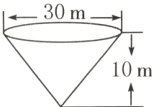
答案： 45km² = 45000000m²　100mm = 0.1m 　45000000×0.1×15% = 675000(m³)　$\frac{1}{3}\times3.14\times(30\div2)^{2}\times10 = 2355(m^{3})$　675000÷2355≈286(个)　大约能装满286个圆锥形蓄水池