2025年乐享暑假生活八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年乐享暑假生活八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 当 $ a $ 为实数时,下列各式:$\sqrt { a + 10 }$,$\sqrt { | a | }$,$\sqrt { a ^ { 2 } }$,$\sqrt { a ^ { 2 } - 1 }$,$\sqrt { a ^ { 2 } + 1 }$,$\sqrt { ( a - 1 ) ^ { 2 } }$ 是二次根式的有(
A.3 个
B.4 个
C.5 个
D.6 个
B
)A.3 个
B.4 个
C.5 个
D.6 个
答案:
解:二次根式的定义是形如$\sqrt{a}(a\geq0)$的代数式。
- $\sqrt{a + 10}$:当$a < -10$时,$a + 10 < 0$,不是二次根式。
- $\sqrt{|a|}$:因为$|a| \geq 0$恒成立,是二次根式。
- $\sqrt{a^2}$:因为$a^2 \geq 0$恒成立,是二次根式。
- $\sqrt{a^2 - 1}$:当$a^2 < 1$,即$-1 < a < 1$时,$a^2 - 1 < 0$,不是二次根式。
- $\sqrt{a^2 + 1}$:因为$a^2 + 1 \geq 1 > 0$恒成立,是二次根式。
- $\sqrt{(a - 1)^2}$:因为$(a - 1)^2 \geq 0$恒成立,是二次根式。
综上,是二次根式的有$\sqrt{|a|}$,$\sqrt{a^2}$,$\sqrt{a^2 + 1}$,$\sqrt{(a - 1)^2}$,共4个。
答案:B
- $\sqrt{a + 10}$:当$a < -10$时,$a + 10 < 0$,不是二次根式。
- $\sqrt{|a|}$:因为$|a| \geq 0$恒成立,是二次根式。
- $\sqrt{a^2}$:因为$a^2 \geq 0$恒成立,是二次根式。
- $\sqrt{a^2 - 1}$:当$a^2 < 1$,即$-1 < a < 1$时,$a^2 - 1 < 0$,不是二次根式。
- $\sqrt{a^2 + 1}$:因为$a^2 + 1 \geq 1 > 0$恒成立,是二次根式。
- $\sqrt{(a - 1)^2}$:因为$(a - 1)^2 \geq 0$恒成立,是二次根式。
综上,是二次根式的有$\sqrt{|a|}$,$\sqrt{a^2}$,$\sqrt{a^2 + 1}$,$\sqrt{(a - 1)^2}$,共4个。
答案:B
2. $( \sqrt { 3 } ) ^ { 2 }$ 的值是(
A.$\sqrt { 3 }$
B.3
C.$\pm 3$
D.9
B
)A.$\sqrt { 3 }$
B.3
C.$\pm 3$
D.9
答案:
解:$(\sqrt{3})^2 = 3$
答案:B
答案:B
3. 若式子 $\sqrt { x - 1 }$ 在实数范围内有意义,则 $ x $ 的取值范围在数轴上可表示为(
D
)
答案:
要使式子$\sqrt{x - 1}$在实数范围内有意义,被开方数须是非负数,即$x - 1\geq0$,解得$x\geq1$。
在数轴上表示$x\geq1$时,起点为1,且为实心点,方向向右。观察选项,D选项符合。
D
在数轴上表示$x\geq1$时,起点为1,且为实心点,方向向右。观察选项,D选项符合。
D
4. 若 $\frac { \sqrt { 1 - x } } { 1 - | x | }$ 在实数范围内有意义,则 $ x $ 的取值范围是(
A.$- 1 < x < 1$
B.$x \leq 1$
C.$x < 1$ 且 $x \neq 0$
D.$x < 1$ 且 $x \neq - 1$
D
)A.$- 1 < x < 1$
B.$x \leq 1$
C.$x < 1$ 且 $x \neq 0$
D.$x < 1$ 且 $x \neq - 1$
答案:
要使$\frac{\sqrt{1 - x}}{1 - |x|}$在实数范围内有意义,需满足:
1. 分子中被开方数非负:$1 - x \geq 0$,解得$x \leq 1$;
2. 分母不为零:$1 - |x| \neq 0$,即$|x| \neq 1$,解得$x \neq 1$且$x \neq -1$。
综合以上条件,$x$的取值范围是$x < 1$且$x \neq -1$。
D
1. 分子中被开方数非负:$1 - x \geq 0$,解得$x \leq 1$;
2. 分母不为零:$1 - |x| \neq 0$,即$|x| \neq 1$,解得$x \neq 1$且$x \neq -1$。
综合以上条件,$x$的取值范围是$x < 1$且$x \neq -1$。
D
5. 若 $2 < a < 3$,则 $\sqrt { ( 2 - a ) ^ { 2 } } - \sqrt { ( 3 - a ) ^ { 2 } } = $
A.$5 - 2 a$
B.$1 - 2 a$
C.$2 a - 1$
D.$2 a - 5$
D
A.$5 - 2 a$
B.$1 - 2 a$
C.$2 a - 1$
D.$2 a - 5$
答案:
D 解析:因为 $ 2 < a < 3 $,所以 $ \sqrt{(2 - a)^2} - \sqrt{(3 - a)^2} = a - 2 - (3 - a) = a - 2 - 3 + a = 2a - 5 $。
6. 当 $ x $
$\leq 3$
时,$\frac { x - 1 } { \sqrt { x - 3 } }$ 没有意义。
答案:
要使$\frac{x - 1}{\sqrt{x - 3}}$没有意义,需满足分母为零或二次根式的被开方数为负数。
分母$\sqrt{x - 3}$,二次根式有意义的条件是被开方数非负,即$x - 3 \geq 0$,则$x \geq 3$。当分母为零时,$\sqrt{x - 3} = 0$,即$x - 3 = 0$,$x = 3$;当被开方数为负数时,$x - 3 < 0$,即$x < 3$。
综上,当$x \leq 3$时,原式没有意义。
答案:$\leq 3$
分母$\sqrt{x - 3}$,二次根式有意义的条件是被开方数非负,即$x - 3 \geq 0$,则$x \geq 3$。当分母为零时,$\sqrt{x - 3} = 0$,即$x - 3 = 0$,$x = 3$;当被开方数为负数时,$x - 3 < 0$,即$x < 3$。
综上,当$x \leq 3$时,原式没有意义。
答案:$\leq 3$
7. 计算:$( - \sqrt { 5 } ) ^ { 2 } = $
5
;$\sqrt { ( 2 - \pi ) ^ { 2 } } = $$\pi - 2$
。
答案:
$(-\sqrt{5})^2=(\sqrt{5})^2=5$;
因为$2 < \pi$,所以$2 - \pi < 0$,则$\sqrt{(2 - \pi)^2}=|2 - \pi|=\pi - 2$。
$5$;$\pi - 2$
因为$2 < \pi$,所以$2 - \pi < 0$,则$\sqrt{(2 - \pi)^2}=|2 - \pi|=\pi - 2$。
$5$;$\pi - 2$
8. 实数 $ a$,$b $ 对应的点在数轴上的位置如图所示,化简 $\sqrt { a ^ { 2 } - 4 a + 4 } - | a - b | = $
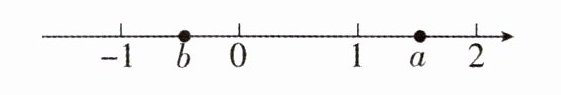
$2 - 2a + b$
。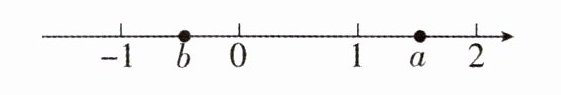
答案:
解:由数轴知:$1 < a < 2$,$-1 < b < 0$
$\sqrt{a^2 - 4a + 4} - |a - b| = \sqrt{(a - 2)^2} - |a - b|$
$\because a - 2 < 0$,$a - b > 0$
$\therefore$原式$= 2 - a - (a - b) = 2 - a - a + b = 2 - 2a + b$
$2 - 2a + b$
$\sqrt{a^2 - 4a + 4} - |a - b| = \sqrt{(a - 2)^2} - |a - b|$
$\because a - 2 < 0$,$a - b > 0$
$\therefore$原式$= 2 - a - (a - b) = 2 - a - a + b = 2 - 2a + b$
$2 - 2a + b$
9. 化简:$\sqrt { x ^ { 2 } + 2 x + 1 } + \sqrt { x ^ { 2 } - 4 x + 4 } ( - 1 < x < 2 ) = $
3
。
答案:
解:$\sqrt{x^2 + 2x + 1} + \sqrt{x^2 - 4x + 4}$
$=\sqrt{(x + 1)^2} + \sqrt{(x - 2)^2}$
因为$-1 < x < 2$,所以$x + 1 > 0$,$x - 2 < 0$。
则原式$=x + 1 + (2 - x)$
$=x + 1 + 2 - x$
$=3$
3
$=\sqrt{(x + 1)^2} + \sqrt{(x - 2)^2}$
因为$-1 < x < 2$,所以$x + 1 > 0$,$x - 2 < 0$。
则原式$=x + 1 + (2 - x)$
$=x + 1 + 2 - x$
$=3$
3
10. 计算:$- \sqrt { ( - 7 ) ^ { 2 } } = $
$-7$
;$\sqrt { ( \sqrt { 7 } - 2 \sqrt { 2 } ) ^ { 2 } } = $$2\sqrt{2} - \sqrt{7}$
。
答案:
$- \sqrt { ( - 7 ) ^ { 2 } } = - \sqrt { 49 } = - 7$;
因为$\sqrt{7} \approx 2.6458$,$2\sqrt{2} \approx 2.8284$,所以$\sqrt{7} - 2\sqrt{2} < 0$,则$\sqrt { ( \sqrt { 7 } - 2 \sqrt { 2 } ) ^ { 2 } } = | \sqrt { 7 } - 2 \sqrt { 2 } | = 2\sqrt{2} - \sqrt{7}$。
$-7$;$2\sqrt{2} - \sqrt{7}$
因为$\sqrt{7} \approx 2.6458$,$2\sqrt{2} \approx 2.8284$,所以$\sqrt{7} - 2\sqrt{2} < 0$,则$\sqrt { ( \sqrt { 7 } - 2 \sqrt { 2 } ) ^ { 2 } } = | \sqrt { 7 } - 2 \sqrt { 2 } | = 2\sqrt{2} - \sqrt{7}$。
$-7$;$2\sqrt{2} - \sqrt{7}$
查看更多完整答案,请扫码查看


