2025年乐享暑假生活八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年乐享暑假生活八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 在$\triangle ABC$中,$D$,$E分别是AB$,$AC$的中点,且$DE = 5cm$,则$BC = $(
A.$5cm$
B.$10cm$
C.$2.5cm$
D.$20cm$
B
)A.$5cm$
B.$10cm$
C.$2.5cm$
D.$20cm$
答案:
解:
∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∵DE=5cm,
∴BC=2×5=10cm。
答案:B
∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∵DE=5cm,
∴BC=2×5=10cm。
答案:B
2. 如图,在四边形$ABCD$中,对角线$AC与BD相交于点O$,下列条件中不能判定四边形$ABCD$是平行四边形的是(

A.$OA = OC$,$OB = OD$
B.$AB// CD$,$AD// CB$
C.$AB = CD$,$AD = CB$
D.$AB// CD$,$AD = CB$
D
)
A.$OA = OC$,$OB = OD$
B.$AB// CD$,$AD// CB$
C.$AB = CD$,$AD = CB$
D.$AB// CD$,$AD = CB$
答案:
解:A. 对角线互相平分的四边形是平行四边形,能判定;
B. 两组对边分别平行的四边形是平行四边形,能判定;
C. 两组对边分别相等的四边形是平行四边形,能判定;
D. 一组对边平行,另一组对边相等的四边形不一定是平行四边形(可能是等腰梯形),不能判定。
答案:D
B. 两组对边分别平行的四边形是平行四边形,能判定;
C. 两组对边分别相等的四边形是平行四边形,能判定;
D. 一组对边平行,另一组对边相等的四边形不一定是平行四边形(可能是等腰梯形),不能判定。
答案:D
3. 如图,平行四边形$ABCD$中,$E是边AB$的中点,$F是对角线BD$的中点,若$EF = 3$,则$BC = $(
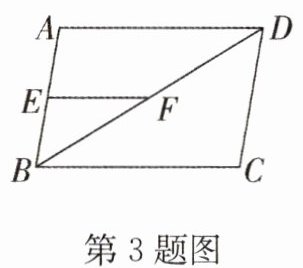
A.$4.5$
B.$5$
C.$5.5$
D.$6$
D
)
A.$4.5$
B.$5$
C.$5.5$
D.$6$
答案:
解:在平行四边形$ABCD$中,$AD// BC$,$AD = BC$。
因为$E$是边$AB$的中点,$F$是对角线$BD$的中点,
所以$EF$是$\triangle ABD$的中位线。
根据三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半,
可得$EF=\dfrac{1}{2}AD$。
已知$EF = 3$,则$\dfrac{1}{2}AD=3$,解得$AD = 6$。
又因为$AD = BC$,所以$BC=6$。
答案:D
因为$E$是边$AB$的中点,$F$是对角线$BD$的中点,
所以$EF$是$\triangle ABD$的中位线。
根据三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半,
可得$EF=\dfrac{1}{2}AD$。
已知$EF = 3$,则$\dfrac{1}{2}AD=3$,解得$AD = 6$。
又因为$AD = BC$,所以$BC=6$。
答案:D
4. 四边形$ABCD$中,对角线$AC$,$BD交于点O$,给出下列四组条件:
①$AB// CD$,$AD// BC$;②$AB// CD$,$\angle BAD = \angle BCD$;
③$AO = CO$,$BO = DO$;④$AB// CD$,$AD = BC$。
一定能判定四边形$ABCD$是平行四边形的条件有(
A.$1$组
B.$2$组
C.$3$组
D.$4$组
①$AB// CD$,$AD// BC$;②$AB// CD$,$\angle BAD = \angle BCD$;
③$AO = CO$,$BO = DO$;④$AB// CD$,$AD = BC$。
一定能判定四边形$ABCD$是平行四边形的条件有(
C
)A.$1$组
B.$2$组
C.$3$组
D.$4$组
答案:
解:①$AB// CD$,$AD// BC$,两组对边分别平行的四边形是平行四边形,能判定;
②$AB// CD$,则$\angle BAD+\angle ADC=180^\circ$,又$\angle BAD = \angle BCD$,所以$\angle BCD+\angle ADC=180^\circ$,可得$AD// BC$,两组对边分别平行的四边形是平行四边形,能判定;
③$AO = CO$,$BO = DO$,对角线互相平分的四边形是平行四边形,能判定;
④$AB// CD$,$AD = BC$,可能是等腰梯形,不能判定。
综上,①②③能判定,共3组。
答案:C
②$AB// CD$,则$\angle BAD+\angle ADC=180^\circ$,又$\angle BAD = \angle BCD$,所以$\angle BCD+\angle ADC=180^\circ$,可得$AD// BC$,两组对边分别平行的四边形是平行四边形,能判定;
③$AO = CO$,$BO = DO$,对角线互相平分的四边形是平行四边形,能判定;
④$AB// CD$,$AD = BC$,可能是等腰梯形,不能判定。
综上,①②③能判定,共3组。
答案:C
5. 如图,在$□ ABCD$中,$AB = 2AD$,$\angle A = 60^{\circ}$,$E$,$F分别为AB$,$CD$的中点,$EF = 1cm$,那么对角线$BD$的长度是(
A.$1cm$
B.$2cm$
C.$2\sqrt{3}cm$
D.$\sqrt{3}cm$
D
)A.$1cm$
B.$2cm$
C.$2\sqrt{3}cm$
D.$\sqrt{3}cm$
答案:
解:
∵四边形ABCD是平行四边形,E、F分别为AB、CD中点,
∴EF=AD(平行四边形对边中点连线等于边长),
∵EF=1cm,
∴AD=1cm.
∵AB=2AD,
∴AB=2cm.
过D作DG⊥AB于G,
在Rt△ADG中,∠A=60°,AD=1cm,
∴AG=AD·cos60°=1×$\frac{1}{2}$=$\frac{1}{2}$cm,
DG=AD·sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$cm.
∵AB=2cm,
∴BG=AB-AG=2-$\frac{1}{2}$=$\frac{3}{2}$cm.
在Rt△BDG中,BD=$\sqrt{DG^2+BG^2}$=$\sqrt{(\frac{\sqrt{3}}{2})^2+(\frac{3}{2})^2}$=$\sqrt{\frac{3}{4}+\frac{9}{4}}$=$\sqrt{3}$cm.
D
∵四边形ABCD是平行四边形,E、F分别为AB、CD中点,
∴EF=AD(平行四边形对边中点连线等于边长),
∵EF=1cm,
∴AD=1cm.
∵AB=2AD,
∴AB=2cm.
过D作DG⊥AB于G,
在Rt△ADG中,∠A=60°,AD=1cm,
∴AG=AD·cos60°=1×$\frac{1}{2}$=$\frac{1}{2}$cm,
DG=AD·sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$cm.
∵AB=2cm,
∴BG=AB-AG=2-$\frac{1}{2}$=$\frac{3}{2}$cm.
在Rt△BDG中,BD=$\sqrt{DG^2+BG^2}$=$\sqrt{(\frac{\sqrt{3}}{2})^2+(\frac{3}{2})^2}$=$\sqrt{\frac{3}{4}+\frac{9}{4}}$=$\sqrt{3}$cm.
D
6. 如图,在四边形$ABCD$中,$AB = CD$,再添加一个条件
$AB// CD$
(写出一个即可),可使四边形$ABCD$是平行四边形。(图中不再添加辅助线)
答案:
$AB// CD$
7. 一块等腰三角形空地$ABC$,如图,已知点$D$,$E分别是边AB$,$AC$的中点,量得$AC = 10$米,$AB = BC = 6$米,若用篱笆围成四边形$BCED$来放养小鸡,则需要篱笆

17
米。
答案:
解:因为点D,E分别是边AB,AC的中点,所以DE是△ABC的中位线。
根据三角形中位线定理,DE = $\frac{1}{2}$BC。
已知AB = BC = 6米,所以DE = $\frac{1}{2}×6 = 3$米。
又因为D是AB中点,所以BD = $\frac{1}{2}$AB = $\frac{1}{2}×6 = 3$米。
E是AC中点,AC = 10米,所以EC = $\frac{1}{2}$AC = $\frac{1}{2}×10 = 5$米。
四边形BCED的篱笆长度为BC + CE + DE + BD = 6 + 5 + 3 + 3 = 17米。
17
根据三角形中位线定理,DE = $\frac{1}{2}$BC。
已知AB = BC = 6米,所以DE = $\frac{1}{2}×6 = 3$米。
又因为D是AB中点,所以BD = $\frac{1}{2}$AB = $\frac{1}{2}×6 = 3$米。
E是AC中点,AC = 10米,所以EC = $\frac{1}{2}$AC = $\frac{1}{2}×10 = 5$米。
四边形BCED的篱笆长度为BC + CE + DE + BD = 6 + 5 + 3 + 3 = 17米。
17
查看更多完整答案,请扫码查看


