《2025年乐享暑假生活八年级数学人教版》

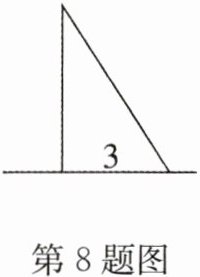
8. 《九章算术》中有“折竹抵地”问题：“今有竹高一丈,末折抵地,去根三尺,问折者高几何？”题意：有一根竹子原来高 1 丈(1 丈= 10 尺),中部有一处折断,竹梢触地面处离竹根 3 尺,试问折断处离地面多高？如图,设折断处距离地面 a 尺,根据题意,则可列方程：$a^{2}+3^{2}=(10 - a)^{2}$。

答案： 设折断处距离地面$a$尺，则折断后竹梢部分长度为$(10 - a)$尺。根据勾股定理，可列方程：$a^{2}+3^{2}=(10 - a)^{2}$
$a^{2}+3^{2}=(10 - a)^{2}$

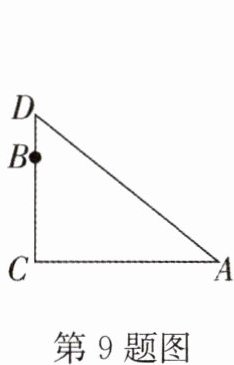
9. 在一棵树的 5 米高 B 处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到 A 处(离树 10 米)的池塘边,另一只爬到树顶 D 后直接跃到 A 处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高______米。

7.5

答案： 解：设树高为 $ h $ 米，则 $ DC = h $ 米，$ BD = (h - 5) $ 米。
由题意，第一只猴子经过的距离为 $ BC + CA = 5 + 10 = 15 $ 米。
第二只猴子经过的距离为 $ BD + DA = (h - 5) + DA $，且两只猴子距离相等，故 $ DA = 15 - (h - 5) = 20 - h $。
在 $ \text{Rt}\triangle DCA $ 中，由勾股定理得：$ DC^2 + CA^2 = DA^2 $，
即 $ h^2 + 10^2 = (20 - h)^2 $。
展开得 $ h^2 + 100 = 400 - 40h + h^2 $，
化简得 $ 40h = 300 $，解得 $ h = 7.5 $。
7.5

10. 已知某直角三角形的一条直角边和斜边长分别为 5 和 13.
(1)该直角三角形的另一条直角边长为12；
(2)该直角三角形斜边上的高为$\frac{60}{13}$。

答案：
(1)设另一条直角边长为$a$，根据勾股定理$a^2 + 5^2 = 13^2$，即$a^2 = 13^2 - 5^2 = 169 - 25 = 144$，解得$a = 12$。
(2)设斜边上的高为$h$，三角形面积为$\frac{1}{2} × 5 × 12 = 30$，又因为面积也可表示为$\frac{1}{2} × 13 × h$，所以$\frac{1}{2} × 13 × h = 30$，解得$h = \frac{60}{13}$。
(1)12；
(2)$\frac{60}{13}$

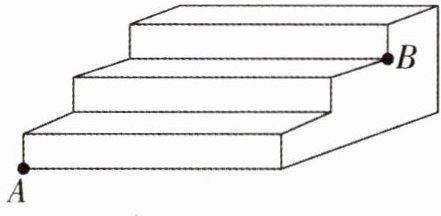
11. 如图,台阶阶梯每一层高 20 cm,宽 40 cm,长 50 cm,一只蚂蚁从 A 点爬到 B 点,最短路程是多少？

答案： 解：将台阶展开，水平方向总长度为 $40×3 = 120\,\text{cm}$，垂直方向总高度为 $20×3 = 60\,\text{cm}$，台阶长为 $50\,\text{cm}$。
展开后，A、B两点在同一平面内，横向距离为 $120\,\text{cm}$，纵向距离为 $50\,\text{cm}$（长），垂直高度已转化为水平方向，此时最短路径为直角三角形斜边，两直角边分别为 $120\,\text{cm}$ 和 $50\,\text{cm}$。
根据勾股定理：$AB = \sqrt{120^2 + 50^2} = \sqrt{14400 + 2500} = \sqrt{16900} = 130\,\text{cm}$。
答：最短路程是 $130\,\text{cm}$。

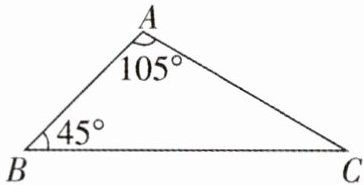
12. 如图,在$\triangle ABC$中,$\angle B= 45^{\circ}$,$\angle A= 105^{\circ}$,$AC= 4$,求 BC 的长。

答案： 解：过点$A$作$AD\perp BC$于点$D$。
在$\triangle ABC$中，$\angle BAC = 105^{\circ}$，$\angle B = 45^{\circ}$，则$\angle C=180^{\circ}-\angle BAC - \angle B=180^{\circ}-105^{\circ}-45^{\circ}=30^{\circ}$。
在$Rt\triangle ADC$中，$\angle C = 30^{\circ}$，$AC = 4$，所以$AD=\frac{1}{2}AC = 2$，$CD=AC\cdot\cos30^{\circ}=4×\frac{\sqrt{3}}{2}=2\sqrt{3}$。
在$Rt\triangle ABD$中，$\angle B = 45^{\circ}$，$AD = 2$，所以$BD=AD = 2$。
因此$BC=BD + CD=2 + 2\sqrt{3}$。
$2+2\sqrt{3}$