《2025年作业本江西教育出版社九年级物理上册教科版》

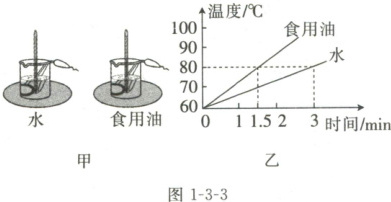
9. 图1-3-3甲所示的是“探究水和食用油的吸放热性能”的实验装置，实验中用电加热器给水和食用油加热。
(1) 实验中应保证水和食用油的初温与质量(选填“质量”或“体积”)都相同。
(2) 实验中用相同(选填“相同”或“不同”)规格的电加热器加热相同的时间，可以认为水吸收的热量等于(选填“大于”“小于”或“等于”)食用油吸收的热量。
(3) 记录实验数据并绘制出两种液体的温度随加热时间变化的图像如图1-3-3乙所示。由图像可知，水和食用油升高相同的温度，水需要加热的时间更长，说明它的吸热能力更强。
(4) 实验发现不同物质在质量相同、升高的温度相同时，吸收的热量一般不同。为了表示不同物质的吸放热性能，物理学中引入了比热容这个物理量。
(5) 由图可知，食用油的比热容$c_油=$2.1×10³$J/(kg·\degreeC)$。

答案：
(1)质量
(2)相同；等于
(3)水；强
(4)比热容
(5)2.1×10³

10. 某同学用燃气灶烧水给餐具消毒。已知密闭锅内水的质量为$5\ kg$，水的初温为20℃，当水刚好烧开时，共消耗了$0.05\ m^3$天然气，该燃气灶烧水的热效率为$84\%$。已知水的比热容为4.2×10^3\ J/(kg·℃)，天然气的热值为$4.0×10^7\ J/m^3$。求：
(1) $0.05\ m^3$天然气完全燃烧放出的热量；
(2) 以上过程中，水吸收的热量；
(3) 锅内水烧开时的温度。

答案： 1. （1）解：根据公式$Q_{放}=Vq$（其中$V$是燃料体积，$q$是燃料热值），已知$V = 0.05m^{3}$，$q = 4.0×10^{7}J/m^{3}$，则$0.05m^{3}$天然气完全燃烧放出的热量：
$Q_{放}=Vq=0.05m^{3}×4.0×10^{7}J/m^{3}=2×10^{6}J$。
2. （2）解：已知热效率$\eta=\frac{Q_{吸}}{Q_{放}}$，$\eta = 84\%$，$Q_{放}=2×10^{6}J$，则水吸收的热量：
$Q_{吸}=\eta Q_{放}=84\%×2×10^{6}J = 1.68×10^{6}J$。
3. （3）解：根据公式$Q_{吸}=cm(t - t_{0})$（其中$c$是比热容，$m$是质量，$t$是末温，$t_{0}$是初温），已知$c = 4.2×10^{3}J/(kg·^{\circ}C)$，$m = 5kg$，$t_{0}=20^{\circ}C$，$Q_{吸}=1.68×10^{6}J$，则：
$t=\frac{Q_{吸}}{cm}+t_{0}=\frac{1.68×10^{6}J}{4.2×10^{3}J/(kg·^{\circ}C)×5kg}+20^{\circ}C$
$=\frac{1.68×10^{6}J}{2.1×10^{4}J/^{\circ}C}+20^{\circ}C$
$ = 80^{\circ}C+20^{\circ}C=100^{\circ}C$。
综上，答案依次为：（1）$2×10^{6}J$；（2）$1.68×10^{6}J$；（3）$100^{\circ}C$。