第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 物体吸收或放出热量的多少,不仅与其
质量
及温度变化量
有关,还与它是什么物质
有关。
答案:
质量;温度变化量;物质
2. 如果质量为$m$的某种物质从外界吸收的热量为$Q$,温度升高了$\Delta t$,那么
Q/(mΔt)
即是这种物质的比热容,用符号c
表示,单位是焦每千克摄氏度,符号是J/(kg·℃)
。比热容是描述物质的吸热能力
或放热能力
的物理量。
答案:
Q/(mΔt);c;J/(kg·℃);吸热能力;放热能力
3. 水的比热容是
4.2×10³J/(kg·℃)
。它表示的物理意义是1kg
水温度升高(或降低)1℃
吸收(或放出)的热量是4.2×10³J
。
答案:
4.2×10³J/(kg·℃);1kg;1℃;4.2×10³J
4. 2024年9月22日,中国科学院合肥物质科学研究院强磁场科学中心自主研制的水冷磁体(图1-3-1)取得重大突破。磁体在工作时会产生大量的热量,需要用高速流动的水来冷却,这是因为水的

比热容
大。该装置内的水使用一段时间后质量减少了,其比热容不变
(选填“变大”“变小”或“不变”)。
答案:
比热容;不变
5. “曲水流觞”是古代文人墨客诗酒唱酬的一种雅事。将酒盏漂浮在清冽的溪水上随溪流动,会降低酒的温度,这是通过
热传递
的方式改变酒的内能。酒盏里质量为100 g的酒在漂流过程中,温度从30℃降低至25℃,会放出1700
J的热量。[c_酒$=3.4×10^3\ J/(kg·℃)]$
答案:
热传递;1700
解析:
1. 酒盏漂浮在溪水上,酒与溪水之间存在温度差,通过热传递的方式改变酒的内能,使酒的温度降低。
2. 已知酒的质量$m = 100\ g=0.1\ kg$,初温t_0=30\ \degreeC,末温t = 25\ \degreeC,比热容c_酒=3.4×10^3\ J/(kg·\degreeC)。
根据热量计算公式$Q_{放}=cm(t_0 - t)$,可得:
Q_{放}=3.4×10^3\ J/(kg·\degreeC)×0.1\ kg×(30\ \degreeC - 25\ \degreeC)=3.4×10^3×0.1×5=1700\ J。
解析:
1. 酒盏漂浮在溪水上,酒与溪水之间存在温度差,通过热传递的方式改变酒的内能,使酒的温度降低。
2. 已知酒的质量$m = 100\ g=0.1\ kg$,初温t_0=30\ \degreeC,末温t = 25\ \degreeC,比热容c_酒=3.4×10^3\ J/(kg·\degreeC)。
根据热量计算公式$Q_{放}=cm(t_0 - t)$,可得:
Q_{放}=3.4×10^3\ J/(kg·\degreeC)×0.1\ kg×(30\ \degreeC - 25\ \degreeC)=3.4×10^3×0.1×5=1700\ J。
6. 将的水倒掉一半,剩下的水的比热容是
$4.2×10^{3}\ J/(kg·^{\circ}C)$
;在标准大气压下,初温为30℃、质量为的水吸收$4.2×10^{4}$
J的热量后温度升高20℃。
答案:
比热容是物质的一种特性,与物质的质量无关,所以将$4\ kg$的水倒掉一半,剩下的水的比热容不变,仍然为$4.2×10^{3}\ J/(kg·^{\circ}C)$。
$m = 500\ g = 0.5\ kg$,$c = 4.2×10^{3}\ J/(kg·^{\circ}C)$,$\Delta t = 20\ ^{\circ}C$。
根据热量计算公式$Q = cm\Delta t$可得:
$Q = 4.2×10^{3}\ J/(kg·^{\circ}C)×0.5\ kg×20\ ^{\circ}C = 4.2×10^{4}\ J$。
故答案为:$4.2×10^{3}\ J/(kg·^{\circ}C)$;$4.2×10^{4}$。
$m = 500\ g = 0.5\ kg$,$c = 4.2×10^{3}\ J/(kg·^{\circ}C)$,$\Delta t = 20\ ^{\circ}C$。
根据热量计算公式$Q = cm\Delta t$可得:
$Q = 4.2×10^{3}\ J/(kg·^{\circ}C)×0.5\ kg×20\ ^{\circ}C = 4.2×10^{4}\ J$。
故答案为:$4.2×10^{3}\ J/(kg·^{\circ}C)$;$4.2×10^{4}$。
7. 在标准大气压下,初温为30℃、质量为$1\ kg$的水吸收$3.36×10^5\ J$的热量后温度升高
70
℃。
答案:
已知:水的质量$m = 1\ kg$,初温t_0 = 30\ \degreeC,吸收的热量$Q_{吸} = 3.36×10^5\ J$,水的比热容c = 4.2×10^3\ J/(kg·\degreeC)。
根据吸热公式$Q_{吸} = cm\Delta t$,可得温度升高量$\Delta t = \frac{Q_{吸}}{cm}$。
代入数据:\Delta t = \frac{3.36×10^5\ J}{4.2×10^3\ J/(kg·\degreeC)×1\ kg} = 80\ \degreeC。
此时末温t = t_0 + \Delta t = 30\ \degreeC + 80\ \degreeC = 110\ \degreeC。
但在标准大气压下,水的沸点为100\ \degreeC,水沸腾后温度不再升高,所以水实际升高的温度为100\ \degreeC - 30\ \degreeC = 70\ \degreeC。
70
根据吸热公式$Q_{吸} = cm\Delta t$,可得温度升高量$\Delta t = \frac{Q_{吸}}{cm}$。
代入数据:\Delta t = \frac{3.36×10^5\ J}{4.2×10^3\ J/(kg·\degreeC)×1\ kg} = 80\ \degreeC。
此时末温t = t_0 + \Delta t = 30\ \degreeC + 80\ \degreeC = 110\ \degreeC。
但在标准大气压下,水的沸点为100\ \degreeC,水沸腾后温度不再升高,所以水实际升高的温度为100\ \degreeC - 30\ \degreeC = 70\ \degreeC。
70
8. 图1-3-2所示的是我国先秦时期的蒸食用具,它由青铜材料铸造而成,分为上、下两部分:上半部是甑(zèng),底部有网眼,可通蒸汽,内部放置食物;下半部是鬲(gé),样子像鼎,用于煮水。下列说法错误的是(
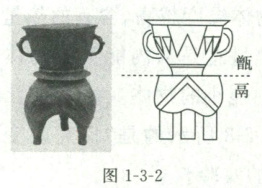
A.鬲内的水沸腾后,继续加热,水温将保持不变,内能也不变
B.水沸腾后,甑周围冒出的“白气”是由水蒸气放热形成的
C.停止加热后,鬲慢慢变凉,这是通过热传递的方式改变鬲的内能
D.停止加热后,甑比盛有水的鬲降温更快,主要原因是青铜的比热容比水小,温度变化更显著
A
)
A.鬲内的水沸腾后,继续加热,水温将保持不变,内能也不变
B.水沸腾后,甑周围冒出的“白气”是由水蒸气放热形成的
C.停止加热后,鬲慢慢变凉,这是通过热传递的方式改变鬲的内能
D.停止加热后,甑比盛有水的鬲降温更快,主要原因是青铜的比热容比水小,温度变化更显著
答案:
A
查看更多完整答案,请扫码查看


