《2025年作业本江西教育出版社九年级物理上册教科版》

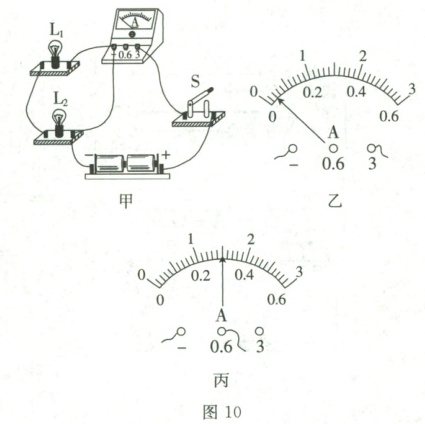
14. 小明和同组的同学们一起做“探究并联电路中的电流关系”的实验，以下是他们的部分实验过程。

(1)连接电路时，开关应处于断开状态。
(2)图10甲所示为小明连接好的电路，他正想闭合开关，另一同学发现电路有错误，提醒他如果闭合开关，电路会处于短路状态。
(3)小明正确连接电路后，闭合开关前，发现电流表指针的位置如图10乙所示，原因是电流表未调零；他改正错误后试触，发现电流表指针的偏转情况仍如图10乙所示。为使读数更精确，他接下来的操作是将电流表的量程换为0~0.6A。
(4)闭合开关进行实验，正确测出电路中的电流，如图10丙所示，则该处电流大小是0.3A。
(5)小亮在实验中用两只规格相同的小灯泡测得的实验数据如下表所示，他由数据得出的结论是在并联电路中，干路电流等于各支路电流之和，且各支路的电流相等。小亮在探究过程中的不妥之处是使用了规格相同的小灯泡（或实验次数太少，结论不具普遍性）(写出一条即可)。

答案：
(1)断开
(2)短路
(3)电流表未调零；将电流表的量程换为0~0.6A
(4)0.3
(5)使用了规格相同的小灯泡（或实验次数太少，结论不具普遍性）

15. 新型节能燃气灶能够提高热效率，减少能源消耗和环境污染。用旧燃气灶将质量为5 kg、初温为20 ℃的水加热到100 ℃，消耗了0.14 $m^{3}$的天然气。已知天然气的热值$q=3×10^{7} J/m^{3}$，水的比热容$c=4.2×10^{3} J/(kg· ^{\circ}C)$。
(1)水吸收的热量是多少?
(2)假设0.14 $m^{3}$的天然气完全燃烧，燃气灶烧水的效率是多少?
(3)如果新型节能燃气灶的效率能够提升到70％，同样将质量为5 kg、初温为20 ℃的水加热到100 ℃，可以节省多少立方米的天然气?

答案：
(1)水吸收的热量：$Q_{吸}=cm(t-t_{0})=4.2×10^{3}J/(kg·^{\circ}C)×5kg×(100^{\circ}C - 20^{\circ}C)=1.68×10^{6}J$
(2)天然气完全燃烧放出的热量：$Q_{放}=Vq=0.14m^{3}×3×10^{7}J/m^{3}=4.2×10^{6}J$
燃气灶烧水的效率：$\eta=\frac{Q_{吸}}{Q_{放}}×100\%=\frac{1.68×10^{6}J}{4.2×10^{6}J}×100\% = 40\%$
(3)由$\eta=\frac{Q_{吸}}{Q_{放}}$得，效率提升后需要天然气完全燃烧放出的热量：$Q_{放}'=\frac{Q_{吸}}{\eta'}=\frac{1.68×10^{6}J}{70\%}=2.4×10^{6}J$
需要天然气的体积：$V'=\frac{Q_{放}'}{q}=\frac{2.4×10^{6}J}{3×10^{7}J/m^{3}}=0.08m^{3}$
节省天然气的体积：$\Delta V=V - V'=0.14m^{3}-0.08m^{3}=0.06m^{3}$
(1)$1.68×10^{6}J$
(2)$40\%$
(3)$0.06m^{3}$