2025年成才之路高中新课程学习指导高中物理必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中物理必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
典题$2$:投壶是从先秦延续至清末的中国传统礼仪和宴饮游戏,《礼记传》中提到:“投壶,射之细也。宴饮有射以乐宾,以习容而讲艺也。”如图所示,甲、乙两人沿水平方向各投出一支箭,箭尖插入壶中时与水平面的夹角分别为$53°$和$37°$;已知两支箭质量相同,忽略空气阻力、箭长、壶口大小等因素的影响,$\sin 37° = 0.6, \cos 37° = 0.8$。下列说法正确的是 (
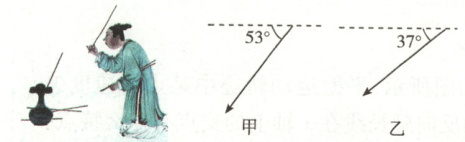
A.若两人站在距壶相同水平距离处投壶,甲所投箭的初速度比乙的小
B.若两人站在距壶相同水平距离处投壶,乙所投的箭在空中运动时间比甲的长
C.若箭在竖直方向下落的高度相等,则甲所射箭落入壶口时速度比乙大
D.若箭在竖直方向下落的高度相等,则甲投壶位置距壶的水平距离比乙大
A
)
A.若两人站在距壶相同水平距离处投壶,甲所投箭的初速度比乙的小
B.若两人站在距壶相同水平距离处投壶,乙所投的箭在空中运动时间比甲的长
C.若箭在竖直方向下落的高度相等,则甲所射箭落入壶口时速度比乙大
D.若箭在竖直方向下落的高度相等,则甲投壶位置距壶的水平距离比乙大
答案:
典题2:A设箭的水平初速度为v,入壶时速度与水平方向的夹角为θ,则有$\frac{gt}{v}$ = tanθ,$\frac{\frac{1}{2}gt²}{x}$ = $\frac{h}{x}$ = $\frac{1}{2}$tanθ,由于tan53°>tan37°,所以$\frac{h_甲}{x_甲}$>$\frac{h_乙}{x_乙}$,若两人站在距壶相同水平距离处投壶,即x_甲 = x_乙时,则h_甲>h_乙,根据h = $\frac{1}{2}$gt²,可知t_甲>t_乙,即甲所投的箭在空中运动时间比乙的长;根据x = vt,可知v_甲<v_乙,即甲所投箭的初速度比乙的小,故A正确,B错误;若箭在竖直方向下落的高度相等,即h_甲 = h_乙,则x_甲<x_乙,即甲投位置距壶的水平距离比乙小;根据h = $\frac{1}{2}$gt²,可知t_甲 = t_乙,根据x = vt,可知v_甲<v_乙,则射箭落入壶口时的速度$\sqrt{v₀²+(gt)²}$<$\sqrt{v₀²+(gt)²}$,即甲所射箭落入壶口时速度比乙小,故C、D错误。故选A。
跟踪训练$2$:飞镖游戏是一种非常有趣味性的娱乐活动,如图所示,某次飞镖比赛,某选手在距地面某相同的高度,向竖直墙面发射飞镖,每次飞镖均水平射出,且发射点与墙壁距离相同,某两次射出的飞镖插入墙面时速度与水平方向夹角第一次为$30°$和第二次为$60°$,若不考虑所受的空气阻力,则 (
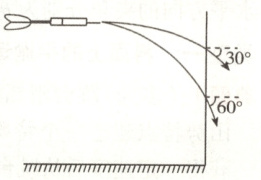
A.两次末速度的反向延长线不一定交于水平位移的中点
B.第一次出手速度比第二次小
C.第一次与第二次运动的时间之比为$1:\sqrt{3}$
D.两次末速度的大小之比为$1:2$
C
)
A.两次末速度的反向延长线不一定交于水平位移的中点
B.第一次出手速度比第二次小
C.第一次与第二次运动的时间之比为$1:\sqrt{3}$
D.两次末速度的大小之比为$1:2$
答案:
跟踪训练2:C根据平抛的推论,末速度的反向延长线一定交于水平位移的中点,故A错误;根据平抛运动的规律,在竖直方向上做自由落体运动,有y = $\frac{1}{2}$gt²,图中可知,y₁<y₂,t₁<t₂,又因为在水平方向做匀速直线运动,有x = vt,则v₁>v₂,故B错误;根据速度偏转角和位移偏转角的关系,tanθ_v = 2tanθ_s,则$\frac{tanθ_{v1}}{tanθ_{v2}}$ = $\frac{tanθ_{s1}}{tanθ_{s2}}$ = $\frac{tan30°}{tan60°}$ = $\frac{1}{3}$,因为水平位移x相同,则$\frac{y₁}{y₂}$ = $\frac{1}{3}$,又有y = $\frac{1}{2}$gt²,所以$\frac{t₁²}{t₂²}$ = $\frac{1}{3}$,故C正确;根据C选项中分析,有$\frac{t₁}{t₂}$ = $\frac{1}{\sqrt{3}}$,则$\frac{v_{y1}}{v_{y2}}$ = $\frac{\sqrt{3}}{1}$,$\frac{v₁}{v₂}$ = $\frac{\sqrt{3}}{1}$·$\frac{v_{x1}}{v_{x2}}$,但是不知道v_x和v_y的具体数量关系,因此无法判断末速度关系,故D错误。故选C。
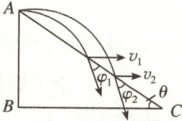
$1$. 如图所示,从倾角为$\theta$且足够长的斜面的顶点$A$,先后将同一小球以不同的初速度水平向右抛出,第一次初速度为$v_1$,小球落到斜面上前一瞬间的速度方向与斜面的夹角为$\varphi_1$,第二次初速度为$v_2$,小球落在斜面上前一瞬间的速度方向与斜面间的夹角为$\varphi_2$,若$v_2 > v_1$,则$\varphi_1$和$\varphi_2$的大小关系是
(
A.$\varphi_1 > \varphi_2$
B.$\varphi_1 < \varphi_2$
C.$\varphi_1 = \varphi_2$
D.无法确定

(
C
)A.$\varphi_1 > \varphi_2$
B.$\varphi_1 < \varphi_2$
C.$\varphi_1 = \varphi_2$
D.无法确定
答案:
1.C根据平抛运动的推论,做平抛(或类平抛)运动的物体在任一时刻或任一位置时,设其速度方向与水平方向的夹角为α,位移与水平方向的夹角为β,则tanα = 2tanβ,由上述关系结合题图中的几何关系可得tan(φ + θ) = 2tanθ,此式表明小球的速度方向与斜面间的夹角φ仅与θ有关,而与初速度无关,因此φ₁ = φ₂,即以不同初速度平抛的物体,落在斜面上各点的速度方向是互相平行的。故选C。
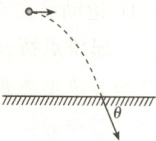
$2$. 如图所示,从某高度水平抛出一小球,经过时间$t$到达地面时,速度与水平方向的夹角为$\theta$,不计空气阻力,重力加速度为$g$,下列说法正确的是
(
A.小球水平抛出时的初速度大小为$g t \tan \theta$
B.小球在$t$时间内的位移方向与水平方向的夹角为$\frac{\theta}{2}$
C.仅小球初速度增大,则平抛运动的时间不变
D.若小球初速度增大,则$\theta$增大

(
C
)A.小球水平抛出时的初速度大小为$g t \tan \theta$
B.小球在$t$时间内的位移方向与水平方向的夹角为$\frac{\theta}{2}$
C.仅小球初速度增大,则平抛运动的时间不变
D.若小球初速度增大,则$\theta$增大
答案:
2.C小球落地时竖直方向的速度v_y = gt,根据题意可得tanθ = $\frac{v_y}{v₀}$,解得v₀ = $\frac{gt}{tanθ}$,A错误;设在t时间内的位移方向与水平方向的夹角为α,根据平抛运动的推论2tanα = tanθ,可知α ≠ $\frac{θ}{2}$,B错误;竖直方向高度不变,根据h = $\frac{1}{2}$gt²,可得t = $\sqrt{\frac{2h}{g}}$,若小球初速度增大,则平抛运动的时间不变,C正确;根据tanθ = $\frac{v_y}{v₀}$ = $\frac{gt}{v₀}$,可知若小球初速度增大,则θ减小,D错误。故选C。
查看更多完整答案,请扫码查看


