2025年成才之路高中新课程学习指导高中物理必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年成才之路高中新课程学习指导高中物理必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
典题1:为了探究平抛运动的规律,某同学用如图(a)所示的装置进行实验。
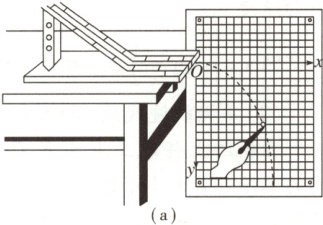
(1)(多选)为了准确地描绘出平抛运动的轨迹,下列要求合理的是 (
A. 小球每次必须从斜槽上同一位置由静止释放
B. 斜槽轨道必须光滑
C. 斜槽轨道末端必须水平
D. 本实验必需的器材还有刻度尺和停表
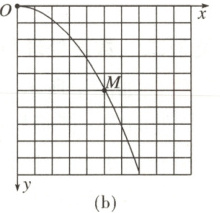
(2)甲同学按正确的操作完成实验并描绘出平抛运动的轨迹,以平抛运动的初始位置$O$为坐标原点建立$xOy$坐标系,如图(b)所示。从运动轨迹上选取多个点,根据其坐标值可以验证轨迹符合$y = ax^{2}$的抛物线。若坐标纸中每个小方格的边长为$L$,根据图中$M$点的坐标值,可以求出$a =$
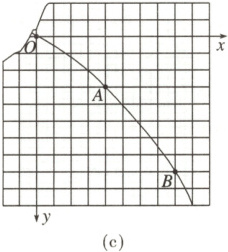
(3)乙同学不小心将记录实验的坐标纸弄破损,导致平抛运动的初始位置缺失。他选取轨迹中任意一点$O$为坐标原点,建立$xOy$坐标系($x$轴沿水平方向、$y$轴沿竖直方向),如图(c)所示。在轨迹中选取$A$、$B$两点,坐标纸中每个小方格的边长仍为$L$,重力加速度为$g$。由此可知:小球从$O$点运动到$A$点所用时间$t_{1}$与从$A$点运动到$B$点所用时间$t_{2}$的大小关系为:$t_{1}$
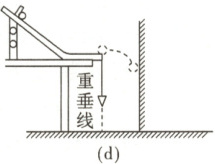
(4)丙同学将实验方案做了改变,如图(d)所示,他把桌子搬到竖直墙的附近,调整好仪器,使从斜槽轨道滚下的小球打在正对的墙上,把白纸和复写纸附在墙上,记录小球的落点。然后等间距地改变桌子与墙的距离,就可以得到多个落点。如果丙同学还有一把刻度尺,他是否可以计算出小球平抛时的初速度?并简要阐述理由。

(1)(多选)为了准确地描绘出平抛运动的轨迹,下列要求合理的是 (
AC
)A. 小球每次必须从斜槽上同一位置由静止释放
B. 斜槽轨道必须光滑
C. 斜槽轨道末端必须水平
D. 本实验必需的器材还有刻度尺和停表
(2)甲同学按正确的操作完成实验并描绘出平抛运动的轨迹,以平抛运动的初始位置$O$为坐标原点建立$xOy$坐标系,如图(b)所示。从运动轨迹上选取多个点,根据其坐标值可以验证轨迹符合$y = ax^{2}$的抛物线。若坐标纸中每个小方格的边长为$L$,根据图中$M$点的坐标值,可以求出$a =$
$\frac{1}{5L}$
,小球平抛运动的初速度$v_{0} =$$\sqrt{\frac{5gL}{2}}$
。(重力加速度为$g$)
(3)乙同学不小心将记录实验的坐标纸弄破损,导致平抛运动的初始位置缺失。他选取轨迹中任意一点$O$为坐标原点,建立$xOy$坐标系($x$轴沿水平方向、$y$轴沿竖直方向),如图(c)所示。在轨迹中选取$A$、$B$两点,坐标纸中每个小方格的边长仍为$L$,重力加速度为$g$。由此可知:小球从$O$点运动到$A$点所用时间$t_{1}$与从$A$点运动到$B$点所用时间$t_{2}$的大小关系为:$t_{1}$
=
$t_{2}$(选填“$>$”“$<$”或“$=$”);小球平抛运动的初速度$v_{0} =$2$\sqrt{2gL}$
,小球平抛运动的初始位置坐标为(−4L,−L)
。
(4)丙同学将实验方案做了改变,如图(d)所示,他把桌子搬到竖直墙的附近,调整好仪器,使从斜槽轨道滚下的小球打在正对的墙上,把白纸和复写纸附在墙上,记录小球的落点。然后等间距地改变桌子与墙的距离,就可以得到多个落点。如果丙同学还有一把刻度尺,他是否可以计算出小球平抛时的初速度?并简要阐述理由。
可以,理由见解析

答案:
(1)AC
(2)$\frac{1}{5L}$ $\sqrt{\frac{5gL}{2}}$
(3)=2$\sqrt{2gL}$(−4L,−L)
(4)可以,理由见解析
解析:
(1)小球每次从斜槽上同一位置由静止释放,滑到斜槽末端时的速率一定,保证平抛初速度不变,描出的是同一轨迹,故A正确;斜槽轨道不必光滑,故B错误;斜槽末端水平,才能保证小球做平抛运动,故C正确;本实验不需要停表,故
D错误。
(2)由y=ax²得a=$\frac{y}{x²}$,将M点坐标(5L,5L)代入得a=
$\frac{5L}{(5L)²}$=$\frac{1}{5L}$,根据x=v₀t,y=$\frac{1}{2}$gt²,联立解得v₀=$\frac{x}{t}$=x$\sqrt{\frac{g}{2y}}$
=x$\sqrt{\frac{g}{2y}}$=5L$\sqrt{\frac{g}{10L}}$=$\sqrt{\frac{5gL}{2}}$
(3)0、A和A、B间水平间距均是4个格,由t=$\frac{x}{v₀}$可知,t₁=
t₂,又yAB−yOA=gT²,解得T=$\sqrt{\frac{y_{AB} - y_{OA}}{g}}$=$\sqrt{\frac{2L}{g}}$,所以v₀=
$\frac{4L}{T}$=2$\sqrt{2gL}$,小球在竖直方向上做自由落体运动,从开始下落,相邻相等时间内竖直位移之比为1:3:5,而yOA:yAB=
3:5,因此初始位置坐标为(−4L,−L)。
(4)可以。用刻度尺测量落点与抛出点之间的竖直距离y,测量墙与桌子的水平距离x,根据y=$\frac{1}{2}$gt²,可得t=$\sqrt{\frac{2y}{g}}$,则
v₀=$\frac{x}{t}$=x$\sqrt{\frac{g}{2y}}$,改变桌子与墙的水平距离x,测量多组x、值,计算多组初速度,取平均值即可。
(1)AC
(2)$\frac{1}{5L}$ $\sqrt{\frac{5gL}{2}}$
(3)=2$\sqrt{2gL}$(−4L,−L)
(4)可以,理由见解析
解析:
(1)小球每次从斜槽上同一位置由静止释放,滑到斜槽末端时的速率一定,保证平抛初速度不变,描出的是同一轨迹,故A正确;斜槽轨道不必光滑,故B错误;斜槽末端水平,才能保证小球做平抛运动,故C正确;本实验不需要停表,故
D错误。
(2)由y=ax²得a=$\frac{y}{x²}$,将M点坐标(5L,5L)代入得a=
$\frac{5L}{(5L)²}$=$\frac{1}{5L}$,根据x=v₀t,y=$\frac{1}{2}$gt²,联立解得v₀=$\frac{x}{t}$=x$\sqrt{\frac{g}{2y}}$
=x$\sqrt{\frac{g}{2y}}$=5L$\sqrt{\frac{g}{10L}}$=$\sqrt{\frac{5gL}{2}}$
(3)0、A和A、B间水平间距均是4个格,由t=$\frac{x}{v₀}$可知,t₁=
t₂,又yAB−yOA=gT²,解得T=$\sqrt{\frac{y_{AB} - y_{OA}}{g}}$=$\sqrt{\frac{2L}{g}}$,所以v₀=
$\frac{4L}{T}$=2$\sqrt{2gL}$,小球在竖直方向上做自由落体运动,从开始下落,相邻相等时间内竖直位移之比为1:3:5,而yOA:yAB=
3:5,因此初始位置坐标为(−4L,−L)。
(4)可以。用刻度尺测量落点与抛出点之间的竖直距离y,测量墙与桌子的水平距离x,根据y=$\frac{1}{2}$gt²,可得t=$\sqrt{\frac{2y}{g}}$,则
v₀=$\frac{x}{t}$=x$\sqrt{\frac{g}{2y}}$,改变桌子与墙的水平距离x,测量多组x、值,计算多组初速度,取平均值即可。
查看更多完整答案,请扫码查看


