2025年期末考向标八年级数学上册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年期末考向标八年级数学上册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
典例1 (邯郸期末)命题“直角三角形的两锐角互余”的逆命题是(
A.如果两个锐角互余,那么这两个角是同一个直角三角形中的角
B.如果两个三角形的锐角互余,则这两个三角形是直角三角形
C.如果两个锐角是直角三角形中的角,那么这两个角互余
D.如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
D
)A.如果两个锐角互余,那么这两个角是同一个直角三角形中的角
B.如果两个三角形的锐角互余,则这两个三角形是直角三角形
C.如果两个锐角是直角三角形中的角,那么这两个角互余
D.如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
答案:
1.D
1. 辨思维 易错题 已知下列命题:①同位角相等;②有一个内角是直角的三角形是直角三角形;③若 $ a > 0,b > 0 $,则 $ a + b > 0 $.其中逆命题属于假命题的有( )
A.0个
B.1个
C.2个
D.3个
A.0个
B.1个
C.2个
D.3个
答案:
1.C
典例2 下列各组图形中,属于全等图形的是( )
A.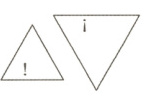
B.
C.
D.
A.
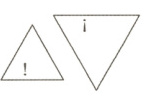
B.

C.

D.

答案:
2.C
2. 下列各组中的两个图形为全等图形的是( )
A.两块三角尺
B.两枚硬币
C.两张 A4 纸
D.两片枫树叶
A.两块三角尺
B.两枚硬币
C.两张 A4 纸
D.两片枫树叶
答案:
2.C
典例3 如图,已知 $ \triangle ABC \cong \triangle EDF $,点 $ A,E $, $ C,F $ 在同一直线上,延长 $ BC $ 交 $ DF $ 于点 $ M $. 若 $ \angle BAC = 70°,\angle EDF = 62° $,则 $ \angle MCF $ 的度数为( )
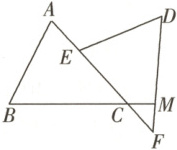
A.$ 38° $
B.$ 48° $
C.$ 62° $
D.$ 70° $

A.$ 38° $
B.$ 48° $
C.$ 62° $
D.$ 70° $
答案:
3.B
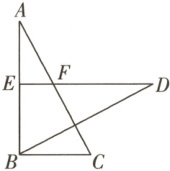
3. 如图,已知 $ \triangle ABC \cong \triangle DEB $,点 $ E $ 在 $ AB $ 上, $ DE $ 与 $ AC $ 相交于点 $ F $.
(1)当 $ DE = 8,BC = 5 $ 时,求线段 $ AE $ 的长.
(2)已知 $ \angle D = 35°,\angle C = 60° $,求 $ \angle DBC $ 与 $ \angle AFD $ 的度数.
(1)当 $ DE = 8,BC = 5 $ 时,求线段 $ AE $ 的长.
(2)已知 $ \angle D = 35°,\angle C = 60° $,求 $ \angle DBC $ 与 $ \angle AFD $ 的度数.

答案:
3.解:
(1)
∵△ABC≌△DEB,DE = 8,BC = 5,
∴AB = DE = 8,BE = BC = 5,
∴AE = AB - BE = 8 - 5 = 3.
(2)
∵△ABC≌△DEB,∠D = 35°,∠C = 60°,
∴∠DBE = ∠C = 60°,∠A = ∠D = 35°,∠ABC = ∠DEB,
∴∠ABC = 180°-∠A - ∠C = 85°,
∴∠DBC = ∠ABC - ∠DBE = 85° - 60° = 25°.
∵∠ABC = 85°,
∴∠DEB = 85°,
∴∠AED = 95°,
∴∠AFD = ∠A + ∠AED = 35° + 95° = 130°.
(1)
∵△ABC≌△DEB,DE = 8,BC = 5,
∴AB = DE = 8,BE = BC = 5,
∴AE = AB - BE = 8 - 5 = 3.
(2)
∵△ABC≌△DEB,∠D = 35°,∠C = 60°,
∴∠DBE = ∠C = 60°,∠A = ∠D = 35°,∠ABC = ∠DEB,
∴∠ABC = 180°-∠A - ∠C = 85°,
∴∠DBC = ∠ABC - ∠DBE = 85° - 60° = 25°.
∵∠ABC = 85°,
∴∠DEB = 85°,
∴∠AED = 95°,
∴∠AFD = ∠A + ∠AED = 35° + 95° = 130°.
典例4 新考向 开放题 (保定期末)如图,点 $ A $, $ B,D $ 在同一条直线上, $ \angle A = \angle CBE = \angle D = 90° $,请你只添加一个条件,使得 $ \triangle ABC \cong \triangle DEB $.
(1)你添加的条件是____. (不添加辅助线)
(2)依据所添条件,判定 $ \triangle ABC $ 与 $ \triangle DEB $ 全等的理由是____.

(1)你添加的条件是____. (不添加辅助线)
(2)依据所添条件,判定 $ \triangle ABC $ 与 $ \triangle DEB $ 全等的理由是____.

答案:
4.
(1)示例:AB = DE
(2)AAS或ASA
(1)示例:AB = DE
(2)AAS或ASA
查看更多完整答案,请扫码查看


